Теплопроводность однородного цилиндрического стержня
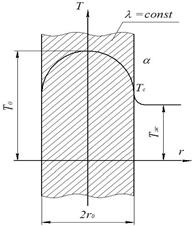
Рассмотрим круглый цилиндр, радиус которого мал по сравнению с длиной цилиндра. При этих условиях температура будет изменяться только вдоль радиуса r (рис. 10). Внутренние источники теплоты равномерно распределены по объему стержня.
Рис. 10 Теплопроводность однородного цилиндрического стержня при наличии внутренних источников тепла
Как и для пластины, задача будет одномерной и симметричной.
Уравнение имеет вид:
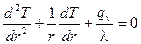 . (1)
. (1)
Граничные условия:
при r = 0 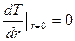 ;
;
при r = r0 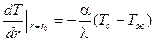 .
.
Необходимо найти: уравнение температурного поля и тепловой поток.
Проведем замену переменных 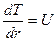 , тогда уравнение (1) примет вид:
, тогда уравнение (1) примет вид:
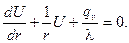 (2)
(2)
Умножим выражение (2) на rdr и получим:
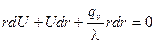 . (3)
. (3)
Первые два слагаемых выражения (3) являются:
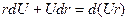 .
.
Тогда выражение (3) можно представить в виде:
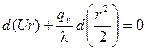 .
.
После интегрирования получим:
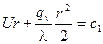 . (4)
. (4)
Разделим выражение на r, получим:
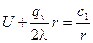 .
.
Вернувшись к замене, получим:
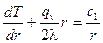 . (5)
. (5)
После второго интегрирования получим:
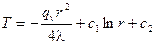 .(6)
.(6)
Определим с1 и с2 из граничных условий.
При r = 0 находим из (5), что с1 = 0.
При r = r0 находим из (5), что 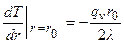 и подставляем в граничные условия:
и подставляем в граничные условия:
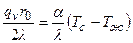 .
.
Откуда:
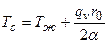 .
.
Из (6) находим с2:
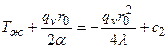 ;
;
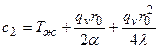 .
.
Уравнение температурного поля:
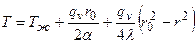 .
.
Дата добавления: 2021-09-07; просмотров: 688;











