Переменный коэффициент теплопроводности

Пусть для плоской стенки l = l₀(1 + bТ),

где l₀ – значение коэффициента теплопроводности при 0°С.

На основании закона Фурье

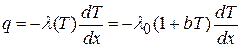. (а)

Разделяя переменные и интегрируя в пределах от х = 0 до х = d в интервале температур от Т_с1 до Т_с2, получаем:

.

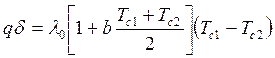Среднеинтегральное значение коэффициента теплопроводности:

.

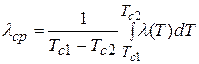Тогда, плотность теплового потока выразится:

.

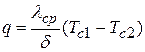Интегрируя (а) в пределах от х = 0 до любой координаты х и в интервале температур от Т_с1 до Т, получаем:

Температура изменяется по кривой:

.

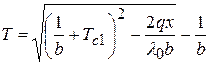Плоская стенка (q_v = 0). Граничные условия третьего рода (теплопередача)

Передача тепла из одной подвижной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей.

Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной подвижной среде.

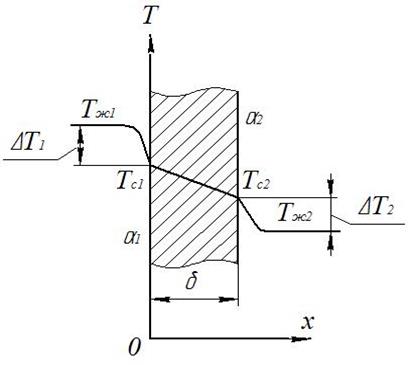
Рис. 4 Теплопередача через плоскую стенку

На рис. 4 показана - плоская стенка толщиной d; Т_ж1 и Т_ж2 - температуры окружающей среды; a₁ и a₂ - коэффициенты теплоотдачи (постоянные). Температура изменения только в направлении, перпендикулярном плоскости стенки.

Необходимо найти: тепловой поток от горячей жидкости к холодной и температуры на поверхностях стенки.

Плотность теплового потока от горячей жидкости к стенке определяется уравнением:

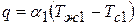. (1)

При стационарном режиме тот же тепловой поток пройдет путем теплопроводности через твердую стенку:

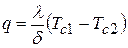. (2)

Тот же тепловой поток передается от второй поверхности стенки к холодной жидкости за счет теплоотдачи:

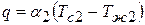. (3)

Эти уравнения можно написать в виде:

.

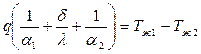Отсюда плотность теплового потока, Вт/м²:

.

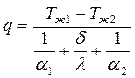Коэффициент теплопередачи, Вт/(м² К):

.

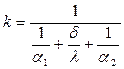Он характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку.

Термическое сопротивление теплопередачи:

.

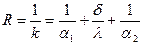Плотность теплового потока выразится:

.

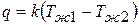Тепловой поток:

.

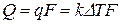Температуры поверхностей однородной стенки можно найти из уравнений (1), (2), (3):

;

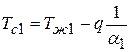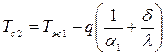или

.

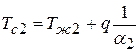(аналогия с электрическим током и напряжением).

Цилиндрическая стенка (q_v = 0)

Уравнение теплопроводности в цилиндрических координатах:

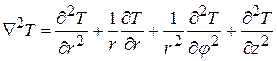
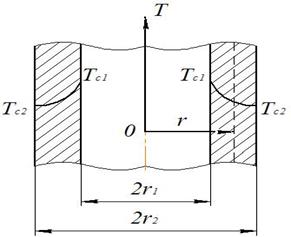
Рис. 5 Теплопроводность цилиндрической стенки

Найти: 1) распределение температур; 2) тепловой поток

Уравнение теплопроводности:

.

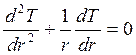Граничные условия 1-го рода:

при r = r₁ Т = Т_с1;

при r = r₂ Т = Т_с2.

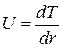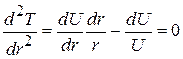Введем новую переменную Þ

Þ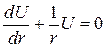

Интегрируем: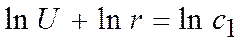

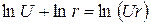Þ .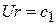

Потенцируя и переходя к первоначальной переменной

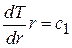Þ .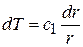

После интегрирования получаем:

.

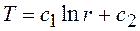Из граничных условий находим постоянные интегрирования:

; .

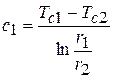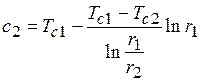Уравнение температурного поля:

.

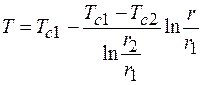Плотность теплового потока зависит от радиуса (гиперболическая кривая) (рис. 5):

.

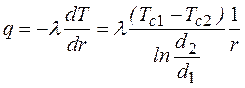Тепловой поток не зависит от радиуса, так как:

,

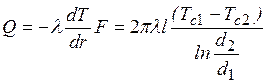где 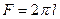- площадь боковой поверхности цилиндра.

Линейная плотность теплового потока:

.

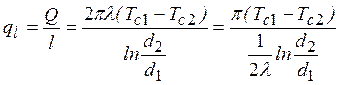Термическое сопротивление цилиндрической стенки:

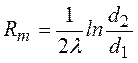
При 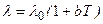линейна плотность теплового потока выразится, как:

,

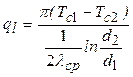где .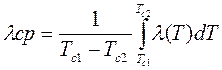

Температурное поле находим из уравнения закона Фурье.

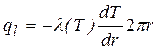(разделяем переменные и интегрируем от r = r₁ до r и от Т = Т_с1 до Т).

.

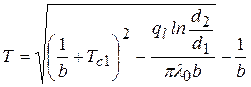Цилиндрическая стенка (q_v = 0). Граничные условия третьего рода (теплопередача).

Рассмотрим однородную цилиндрическую стенку (трубку) с постоянным коэффициентом теплопроводности l (рис. 6).

Необходимо найти: q_l и Т_с1

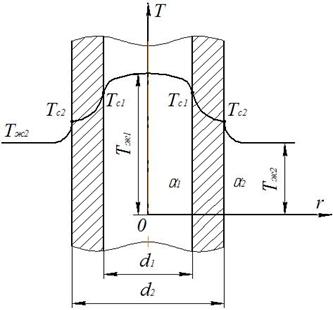Предполагаем, что длина трубы велика по сравнению с толщиной стенки. Тогда потерями теплоты с торцов трубы можно пренебречь. При установившемся тепловом режиме количество теплоты, которое будет передаваться от горячей среды к поверхности стенки, проходить через стенку и отдаваться от стенки к холодной жидкости, будет одно и то же.

Рис. 6 Теплопередача через однородную цилиндрическую стенку

Тепловой поток при теплопередаче через цилиндрическую стенку можно выразить:

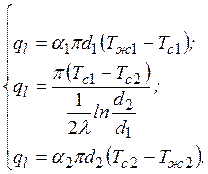
Выразим температурные напоры:

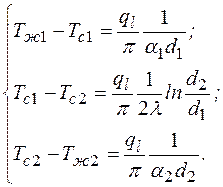
Складывая уравнения, получаем температурный напор:

.

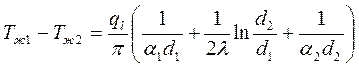Откуда линейная плотность теплового потока находится:

.

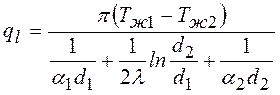Линейный коэффициент теплопередачи:

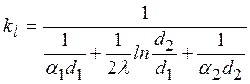, Вт/(м∙К)

Линейная плотность теплового потока:

.

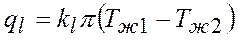Линейное термическое сопротивление:

.

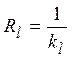Отметим, что линейное термическое сопротивление зависит не только от коэффициентов теплоотдачи a₁, a₂, но и от соответствующих диаметров.