Вывод формулы для определения касательных напряжений при кручении стержня круглого сечения
Теория кручения брусьев круглого или кольцевого сечения основана на следующих положениях:
1. Гипотеза плоских сечений: поперечные сечения вала, плоские до деформации, остаются плоскими и в процессе деформации. Они лишь поворачиваются вокруг оси вала.
2. Радиусы, проведенные в сечении, остаются прямыми и не изменяют своей длины.
3. Расстояния между поперечными сечениями в процессе деформаций остаются постоянными.
Уравнение равновесия при кручении (рис. 6.1) имеет следующий вид:
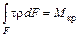 , (6.1)
, (6.1)
где t – касательное напряжение, возникающее в поперечном сечении вала.
|
|
|
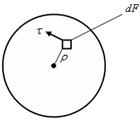
Рис. 6.1
|
|
|
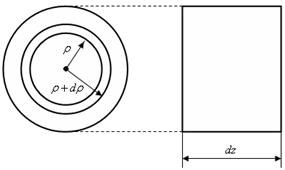
Рис. 6.2
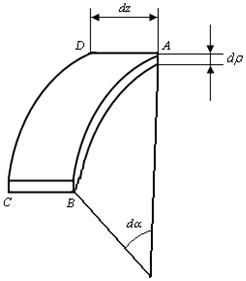
Выделим из окружности в поперечном сечении вала бесконечно-малый элемент и рассмотрим его деформацию. При этом элемент определяется двумя поперечными сечениями, отстоящими на расстояние 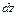 друг от друга. Из него выделяется двумя цилиндрическими поверхностями с радиусами
друг от друга. Из него выделяется двумя цилиндрическими поверхностями с радиусами 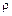 и
и  элементарное кольцо (рис. 6.2).
элементарное кольцо (рис. 6.2).
Выделим из кольца элемент двумя плоскими сечениями, проходящими через ось и образующими между собой угол 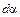 (рис. 6.3).
(рис. 6.3).
|
|
|
|
|
|
|
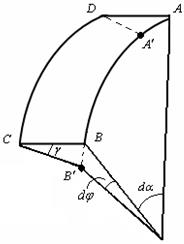
Правое торцевое сечение поворачивается относительно левого на угол 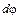 , а образующая
, а образующая 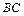 поворачивается на угол
поворачивается на угол  , если считать
, если считать 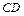 началом отсчета (рис. 6.4).
началом отсчета (рис. 6.4).
Согласно схеме деформаций:
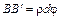 ; (6.2)
; (6.2)
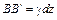 . (6.3)
. (6.3)
Приравняем уравнения (6.2) и (6.3):
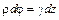 ;
;
 , (6.4)
, (6.4)
где 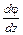 – называется относительным углом закручивания двух смежных сечений. Эта величина аналогична относительному удлинению при растяжении-сжатии
– называется относительным углом закручивания двух смежных сечений. Эта величина аналогична относительному удлинению при растяжении-сжатии 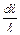 .
.
Элемент 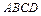 работает в условиях чистого сдвига, а закон Гука при чистом сдвиге имеет вид
работает в условиях чистого сдвига, а закон Гука при чистом сдвиге имеет вид
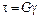 , (6.5)
, (6.5)
где  модуль сдвига (характеристика материала вала).
модуль сдвига (характеристика материала вала).
Подставим выражение (6.4) в (6.5):
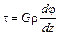 . (6.6)
. (6.6)
Подставим выражение (6.6) в (6.1):
 ; (6.7)
; (6.7)
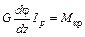 ,
,
или
 . (6.8)
. (6.8)
Подставим (6.8) в (6.6):
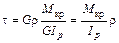 . (6.9)
. (6.9)
В поперечных сечениях вала при кручении возникают касательные напряжения, направление которых в каждой точке перпендикулярно радиусу, соединяющему эту точку с центром тяжести сечения. Значение этого напряжения прямо пропорционально расстоянию до центра тяжести. Следовательно, в центре, при  , касательные напряжения равны нулю, а в точках, расположенных в непосредственной близости от внешней поверхности вала, они максимальны. График изменения касательных напряжений, вдоль какого-либо диаметра носит линейный характер (рис. 6.5).
, касательные напряжения равны нулю, а в точках, расположенных в непосредственной близости от внешней поверхности вала, они максимальны. График изменения касательных напряжений, вдоль какого-либо диаметра носит линейный характер (рис. 6.5).
|
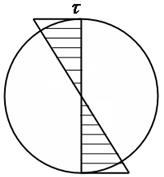
Рис.6.5
Наибольшее напряжение в непосредственной близости от наружной поверхности вала можно получить путем подстановки в выражение (6.9) вместо величины 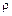 расстояние
расстояние 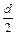 :
:
 , (6.10)
, (6.10)
где 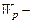 полярный момент сопротивления поперечного сечения;
полярный момент сопротивления поперечного сечения;
 .
.
Выражается 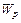 в см3, м3.
в см3, м3.
Для круглого сечения:
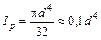 ; (6.11)
; (6.11)
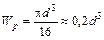 . (6.12)
. (6.12)
Дата добавления: 2020-07-18; просмотров: 841;











