Вдавливание цилиндрического штампа с плоским основанием

При вдавливании жесткого цилиндрического штампа расчетная схема будет иметь вид, представленный рис.25. Рассмотрим вдавливание жесткого цилиндрического штампа в упругое полупространство с силой Р, действующей по оси симметрии z. Это позволит рассматривать эту задачу в цилиндрической системе координат. В этом случае давление по кругу распределится по следующему закону: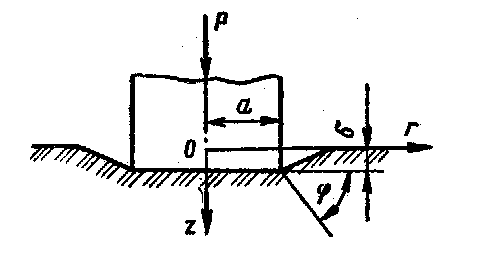

Рис.25 Расчетная схема при вдавливании жесткого штампа

,

а при r = 0:

,

а если r = а, то Р ® ¥.

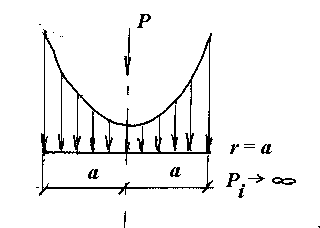Рис.26

Это говорит о том, что давление по площади распределяется неравномерно, с максимальное величиной его на контуре контакта. Графически эта картина выглядит следующим образом (рис.26). На основании изложенного можно сделать вывод, что наиболее опасной зоной является контур давления, где деформации идут независимо; хотя и одновременно с общим деформированием всего объема тела под основанием

цилиндра,т. к. давление по контуру много выше, чем под остальной плоскостью вдавливания, то и касательные напряжения, возникающие в глубине тела по контуру давления, достигают предельных значений много раньше, чем на оси симметрии.

Экспериментами установлено, что такое неравномерное распределение давления по плоскости контакта наблюдается только в первоначальный момент вдавливания. При дальнейшем вдавливании давление по площади можно принять равномерно распределенным. В этом случае давление в любой точке круга можно определить по формуле:

.

В первоначальный момент, когда имеет место неравномерное распределение давления перемещение штампа в полупространство можно определить по формуле:

,

а при равномерном распределении давления величина d может быть определена по формуле:

,

где m - коэффициент Пуассона,

Е - модуль Юнга.

Для правильной оценки поведения горной породы под цилиндрическим штампом необходимо рассмотреть картину напряженного

состояния горной породы вглубь, ниже поверхности контакта. Различаются три области напряженного состояния при вдавливании цилиндрического штампа (см. рис.27). I - область всестороннего сжатия, ограниченная поверхностью s1 = 0, II - в этой области одно из главных напряжений - растягивающее напряжение - больше нуля (s > 0). Эта область ограничена поверхностью s2 = 0.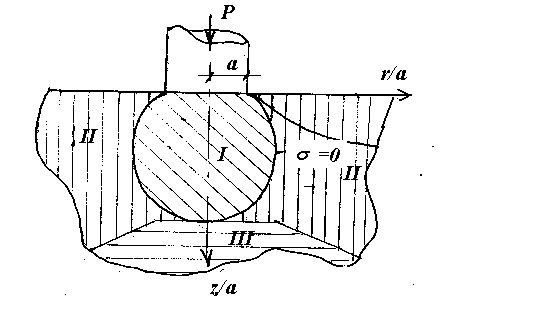

Рис.27

III - эта область лежит ниже границы, где s₂ = 0. Здесь s₁ > 0 и s₂ > 0.

Для оценки величин нормальных напряжений (s₁, s₂, s₃) рассмотрим картину изменений напряжений по оси симметрии z (рис.28).

Рис.28 График изменения напряжений в полупространстве на оси симметрии (r=0)

Из этого графика видно, что напряжения уменьшаются с удалением вглубь от поверхности контакта. Причем, более быстро уменьшаются величины s1 и s2, которые на некоторой глубине переходят, хотя и в незначительные, но в растягивающие. В случае вдавливания цилиндрического Пуассона в горную породу, принято характеризовать ее напряженное состояниекасательными напряжениями, от величины которых во многом зависит энергоемкость процесса разрушения.

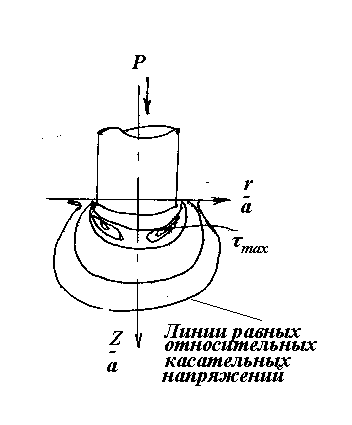Рис.29

На рис.29 показано распределение максимальных касательных напряжений в относительных единицах. Величину максимального касательного напряжения можно определить по формуле С. П. Тимошенко:

,

либо по формуле Р. М. Эйгелеса:

.

Из этих формул видно, что величина максимальных касательных напряжений зависит только от коэффициента Пуассона. Наибольшее значение t_max ,будет иметь место на контуре штампа.