Охлаждение (нагревание) неограниченной пластины
Дана пластина толщиной 2d. Если толщина пластины мала по сравнению с длиной и шириной, то такую пластину считают неограниченной. Коэффициент теплоотдачи a одинаков для всех точек пластины (рис. 12). Изменение  температуры происходит в направлении х. В пространстве задача является одномерной.
температуры происходит в направлении х. В пространстве задача является одномерной.
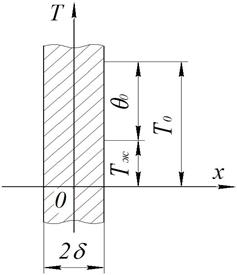
Рис. 12 К охлаждению плоской неограниченной пластины. При τ = 0 задано Т0=const и θ0=const.
Начальное распределение температуры задано некоторой функцией
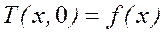 .
.
Охлаждение происходит в среде с постоянной температурой Тж = const. Отсчет температуры пластины для любого момента времени будем вести от температуры окружающей среды Тж, то есть
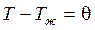 .
.
Дифференциальное уравнение теплопроводности имеет вид:
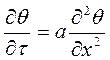 . (1)
. (1)
Начальные условия: при t = 0 θ = θ 0 = f (x) – Тж = F(х).
При заданных условиях охлаждения задача становиться симметричной и начало координат удобно поместить на оси пластины.
При этом граничные условия:
а) на оси пластины при х = 0  ;
;
б) на поверхности пластины при х = d 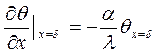 .
.
Для решения дифференциального уравнения применяем метод разделения переменных. При этом решение дифференциальное уравнения ищем в виде произведения двух функций, из которых одна является функцией только времени t, а другая – только х:
 .
.
После подстановки этого выражения в уравнение (1), получим:
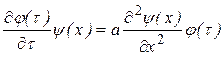 или
или
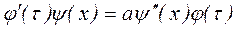 .
.
В этом уравнение легко разделяются переменные
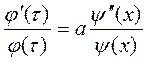 . (2)
. (2)
Левая часть – функция только t, правая только х. Если зафиксировать аргумент х и менять только t, то при любом его значении левая часть уравнения (2) равна постоянной величине, стоящей в правой части, то есть 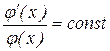 . Аналогично при фиксации t и изменении х правая часть уравнения для любого значения х должна равняться постоянной левой части, которая зависит только от t, то есть
. Аналогично при фиксации t и изменении х правая часть уравнения для любого значения х должна равняться постоянной левой части, которая зависит только от t, то есть 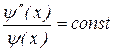 .
.
Так как равенство (2) должно иметь место при любых значениях х и t, то обе его части должны быть равны одной и той же постоянной величине.
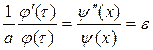 .
.
Нетривиальное решение для функции ᴪ(х) только при e < 0. Положим, что e = - k2 :
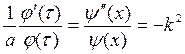 .
.
Система обыкновенных дифференциальных уравнений:
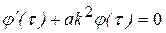 ; (3)
; (3)
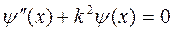 . (4)
. (4)
Постоянная k определяется из граничных условий, а знак «минус» выбирается из физических соображений. Для тепловых процессов, стремящихся к тепловому равновесию, знак может быть только минус.
Уравнению (3) удовлетворяет функция 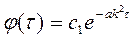 .
.
Уравнение (4) – функция 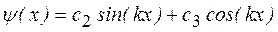 .
.
Дата добавления: 2021-09-07; просмотров: 665;











