Изгиб называют чистым, если изгибающий момент является единственным внутренним усилием, возникающим в поперечном сечении стержня.

В поперечных сечениях стержня наряду с изгибающими моментами возникают также и поперечные силы. Такой изгиб называютпоперечным.Если плоскость действия изгибающего момента (силовая плоскость) проходит через одну из главных центральных осей поперечного сечения стержня, изгиб носит название простого илиплоского.

Если плоскость действия изгибающего момента в сечении не совпадает ни с одной из главных осей сечения, изгиб называют косым. При косом изгибе плоскость деформации не совпадает с силовой плоскостью.

Типы опор балок

Опоры балок, рассматриваемых как плоские системы, бывают трех основных типов.

1. Подвижная шарнирная опора (рис. 5.2 а).Такая опора не препятствует вращению конца балки и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через центр катка. Схематическое изображение подвижной шарнирной опоры дано на рис. 5.2 б.

а) б) в) г)

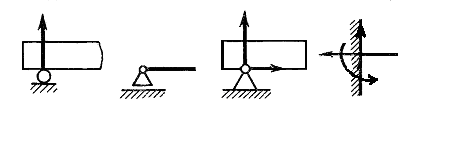
Рис. 5.2.

Подвижные опоры дают возможность балке беспрепятственно изменять свою длину при изменении температуры и тем самым устраняют возможность появления температурных напряжений.

2. Неподвижная шарнирная опора (рис. 5.2 в). Такая опора допускает вращение конца балки, но устраняет поступательное перемещение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие - горизонтальную и вертикальную.

3. Жесткая заделка, или защемление (рис. 5.2 г). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре может в общем случае возникать реакция, которую обычно раскладывают на две составляющие (вертикальную и горизонтальную) и момент защемления (реактивный момент).

Балка с одним заделанным концом называетсяконсольной балкой или простоконсолью.

Если опорные реакции могут быть найдены из одних уравнений статики, то балки называютстатически определимыми. Если же число неизвестных опорных реакций больше, чем число уравнений статики, возможных для данной задачи, то балки называютстатически неопределимыми. Для определения реакций в таких балках приходится составлять дополнительные уравнения - уравнения перемещений.