В результате получили общее решение

<7 8 91011 12 13 >

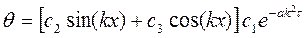. (5)

Для того чтобы уравнение (5) было решением поставленной задачи, его нужно подчинить начальным и граничным условиям.

При х = 0 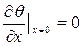, находим

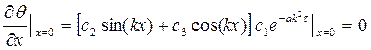Þ 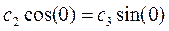Þс₂ = 0

Следовательно, частное решение 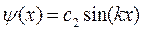– должно быть отброшено как не удовлетворяющее граничным условиям.

Если учесть, что с₂ = 0 и обозначить с₁с₃ = А, то уравнение (5) примет вид:

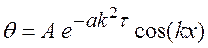При х = d 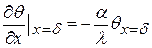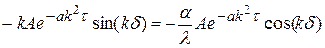Þ 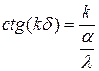½ умножив и разделив на d, получим:

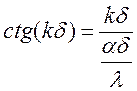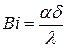- число Био – безразмерный показатель (характеризует соотношения внутреннего и внешнего тепловых сопротивлений).

Если обозначить kd = m, то:

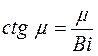(1)

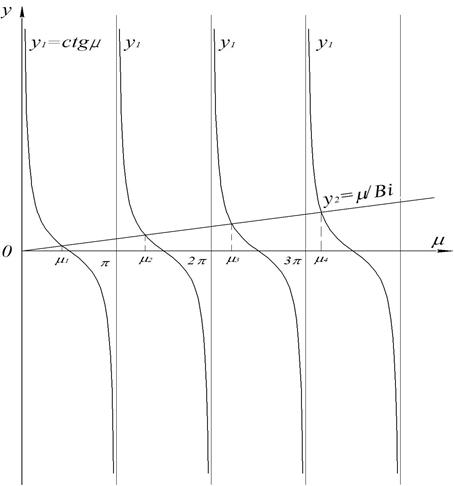
Рис. 13 К решению уравнения (1).

Из анализа этого уравнения следует, что при каждом значении Вi существует бесконечное множество решений. Наиболее просто это равнение решается графическим способом.

Обозначим через y₁= сtg m, ^.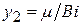

Пересечение котангенсоиды у₁ с прямой у₂ дает бесконечное множество корней характеристического уравнения m₁ < m₂ < m₃ <…<m_n (рис. 13).

Каждому значению Bi отвечает своя совокупность корней уравнения (1). Первые четыре корня такого уравнения приводятся в таблице.

При Вi ® ¥ (внутреннее сопротивление велико по сравнению с внешним) у₂ = 0 – совпадает с осью х и корни будут равны:

m₁= p/2; m₂ = 3p/2; m_n = (2n-1) p/2

При Вi ® 0 (внутреннее сопротивление мало по сравнению с внешним) прямая 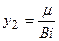совпадает с осью ординат и тангенс угла наклона стремиться к ¥ ® корни равны:

m₁= 0; m₂ = p,…, m_n = (n-1) p.

Следовательно, каждому найденному значению корня m будет соответствовать свое частное распределение температур:

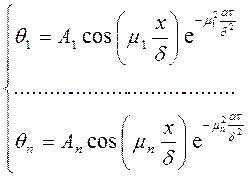, здесь мы учли, что k =μ/δ.

Путем наложения бесконечного числа таких распределений температур можно получить истинное распределение:

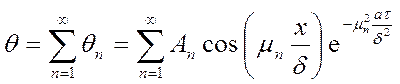.(а)

Постоянная А_n находится из начальных условий:

.

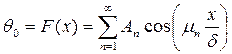Это есть разложение четной функции в ряд Фурье. Есть специальные формулы для определения коэффициентов А_n._.

Если в начальный момент времени t = 0 температура в любой точке пластины распределена равномерно (Т₀ – Т_ж = θ₀ = const), то:

.

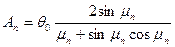Подставляя А_n в выражение (а), получим

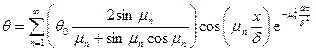.(б)

Уравнение температурного поля (б) целесообразно представить в безразмерной форме. Для этого разделим правую и левую части уравнения на θ₀ (начальная разность температур). При этом обозначим: D_n = А_n / θ₀. Получим:

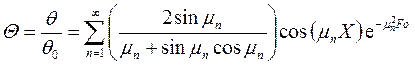, (в)

где Q = θ/θ₀– безразмерная температура; Х = х/d - безразмерная координата; Fo =aτ/δ² – число Фурье, представляющее собой безразмерное время; D_n = А_n / θ₀ – безразмерный коэффициент.

Получим, что температура каждой точки во времени изменяется по экспоненциальному закону. Распределение температуры по координате х (по толщине) – имеет вид косинусоиды с максимумом в центре пластины.

<7 8 91011 12 13 >

Дата добавления: 2021-09-07; просмотров: 388;