Влияние способа закрепления концов стержня на критическую силу

Чаще всего концы стержня закрепляют одним из четырех способов, показанных на рис. 9.4.

Второй способ - шарнирное закрепление обоих концов - рассмотрен нами при выводе формулы Эйлера.

При других способах закрепления обобщенная формула Эйлера для определения критической нагрузки имеет вид

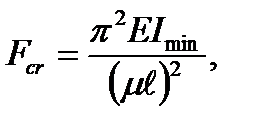(9.7)

где (μ - коэффициент приведения длины стержня), зависящий от способа закрепления концов стержня; 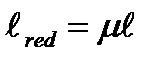- приведенная длина стержня.

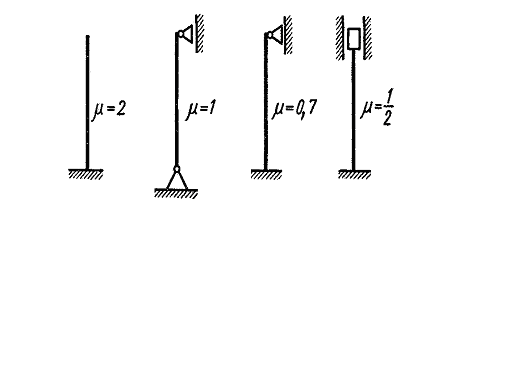
Рис. 9.4.

Формула (9.7) получается, если рассмотреть дифференциальное уравнение продольного изгиба

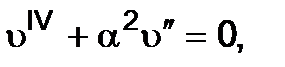
которое следует из уравнения после двукратного дифференцирования.

Решение этого уравнения имеет вид

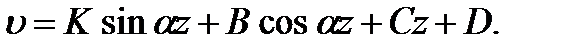
Постоянные К, В, С, D определяются из граничных условий. Например, для третьего случая закрепления (рис. 9.4) при начале координат на нижнем конце имеем ( 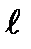- длина стержня):

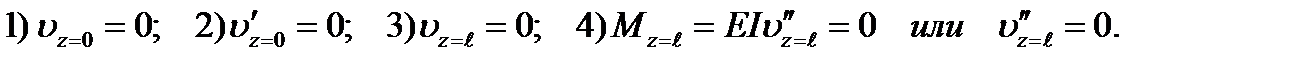
Используя эти условия, получим

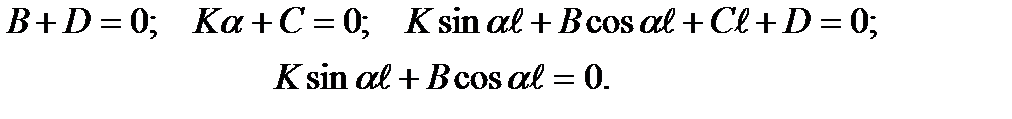
Из математики известно, что система однородных уравнений (т.е. без свободных членов) имеет ненулевое решение только в том случае, когда ее определитель равен нулю:

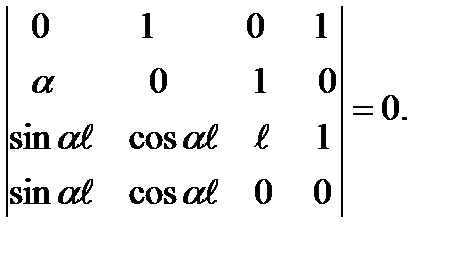
Раскрывая этот определитель, получим 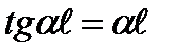. Наименьший корень этого уравнения, отличный от нуля, 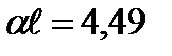, тогда

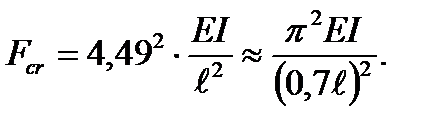
Таким образом, 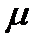= 0,7.

Аналогично получают значения коэффициентов, указанные на рис. 9.4, при других способах закрепления концов стержня.

Как видно из формулы (9.7), чем меньше 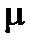, тем больше критическая, а следовательно, и допускаемая нагрузка стержня. Например, нагрузка стержня, заделанного двумя концами, может быть в 16 раз больше нагрузки стержня, заделанного одним концом. Поэтому там, где возможно, следует осуществлять жесткую заделку обоих концов стержня. Однако это не всегда можно осуществить на практике. Элементы, к которым прикрепляются концы рассматриваемого стержня, всегда более или менее упруги, податливы, что вносит некоторую неопределенность в расчет. Поэтому весьма часто даже при жестком соединении концов стержня с другими элементами расчет в запас устойчивости ведут, предполагая шарнирное закрепление обоих концов.