I. Теплопроводность

При создании градиента температуры в металлическом образце концентрации электронов и фононов на холодном конце образца будут меньше соответствующих концентраций на горячем конце образца. Стремление выровнять концентрации по всему объему образца приводит к возникновению направленных потоков фононов и электронов от горячего конца к холодному.

При направленном движении фононов и электронов возможно их рассеяние на других фононах и на дефектах кристаллической структуры. Это ограничивает длину свободного пробега ℓ, которая определяется средней концентрацией рассеивающих центров. При рассеянии на фононах длина свободного пробега обратно пропорциональна средней концентрации фононов <n_ф> и эффективному сечению рассеяния σ*:

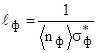и

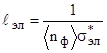
Эффективное сечение рассеяния определяется той областью пространства, которую охватывает атом при своих колебаниях. Если амплитуда колебаний равна А, то σ* ~ πA² – площади сечения сферы радиусом А. При высоких температурах T>Θ_D почти все фононы имеют максимальную энергию и амплитуды колебаний у них одинаковы, что приводит к независимости σ* от температуры. Поэтому при высоких температурах длина свободного пробега как фононов, так и электронов оказывается обратно пропорциональна температуре: ℓ ~ 1/Т.

Вторым механизмом рассеяния является рассеяние на статических дефектах кристаллической решетки – ионах примесей, вакансиях, дислокациях и т.д. Концентрация этих дефектов и эффективное сечение рассеяния практически не зависит от температуры и сказывается только при низких температурах.

Определить теплоту, переносимую фононами и электронами, можно, зная соответствующие коэффициенты теплопроводности.

1. Решеточная теплопроводность.

Представление о тепловом движении атомов в металле как о газе фононов позволяет вычислять решеточную теплопроводность λ согласно молекулярно-кинетической теории газов:

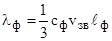
где c_ф – теплоемкость фононов, ℓ_ф – средняя длина свободного пробега фононов, v_зв – средняя скорость фононов, равная скорости звука.

При T>Θ теплоемкость фононного газа равна c_ф = 3Nk, где N – число атомов в единице объема. Это приводит к зависимости λ_ф ~1/T.

С уменьшением температуры теплоемкость начинает зависеть от температуры по кубическому закону Дебая c_ф ~ T³. При этом наиболее существенным фактором являются уменьшение концентрации и увеличение длины свободного пробега фононов. Рост длины свободного пробега фононов ограничен рассеянием на дефектах структуры и при низких температурах ℓ_ф = const. Это означает, что при низких температурах T>Θ фононная теплопроводность пропорциональна кубу температуры λ_ф~T³.

2. Электронная теплопроводность.

Считая электроны газом свободных частиц, можем записать для электронной теплопроводности

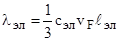
где c_эл – теплоемкость электронов, ℓ_эл – средняя длина свободного пробега электронов, v_F – средняя скорость электронов.

В области высоких температур T>Θ теплоемкость электронного газа линейно зависит от температуры c_эл ~ Т. Это приводит к постоянству коэффициента электронной теплопроводности λ_эл ~ T·1/T = const.

По мере уменьшения температуры и соответствующего уменьшения концентрации фононов электронная теплопроводность растет с понижением температуры как λ_эл ~ 1/T² . При дальнейшем понижении температуры наступает момент, когда длина свободного пробега электронов становится константой. Это приводит к зависимости λ_эл ~ T при T<Θ.

3. Относительный вклад электронной и фононной подсистем.

Для определения вклада колебаний кристаллической решетки (фононов) и свободных электронов в теплопроводность металлов рассмотрим отношение их коэффициентов теплопроводностей

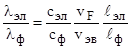
Для чистых металлов c_эл/c_ф ≈ 10^-2, v_F/v_зв ≈ 10³, ℓ_эл/ℓ_ф ≈ 10 и поэтому для них λ_эл/λ_ф~10-100, т.е. в металлах основными переносчиками тепла являются электроны. В неупорядоченных сплавах длины свободного пробега как фононов так и электронов определяются главным образом структурными неоднородностями кристаллической решетки и в них электронная теплопроводность по порядку величину равна решеточной.