Уравнение теплопроводности

Используется метод математической физики (ограничивается расстоянием элементарного объема и малого отрезка времени). Для решения задачи определения температурного поля необходимо иметь дифференциальное уравнение теплопроводности.

Допущения: тело однородно и изотропно, физические параметры – const, деформация объема (в связи с изменением температуры) мала, внутренние источники теплоты распределены равномерно.

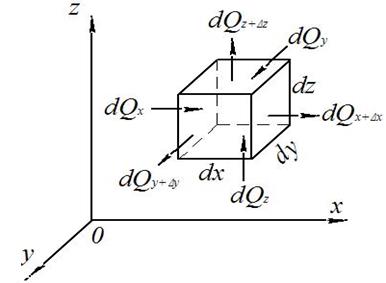
Рис. 2 К выводу дифференциального уравнения теплопроводности

Выделим в объеме тела параллелепипед с гранями dx, dy, dz (рис. 2).

В основе вывода лежит закон сохранения энергии.

,

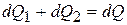где dQ₁ – количество теплоты, введенное теплопроводностью; dQ₂ – количество теплоты за счет внутренних источников энергии; dQ – изменение внутренней энергии (энтальпия).

.

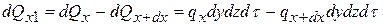Но 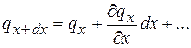можно разложить в ряд Тейлора (как непрерывную функцию) и если ограничиться двумя первыми членами рядя, то:

.

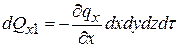Тогда

.

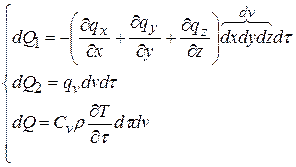
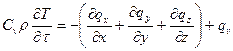В твердых телах по закону Фурье:

.

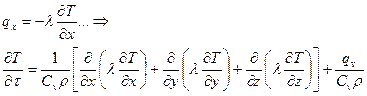
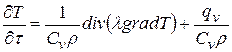Частные случаи.

Дифференциальное уравнение теплопроводности (при l = const)

.

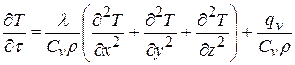При l = const 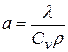– коэффициент температуропроводности (мера теплоинерционности), м²/с.

Уравнение Фурье (без источников тепла q_v = 0):

.

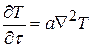Дифференциальное уравнение Пуассона (поле стационарное, q_v ¹ 0)

.

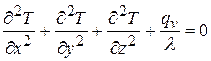Уравнение Лапласа (при стационарной теплопроводности, q_v = 0):

.

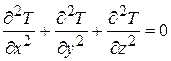В цилиндрической системе координат

.

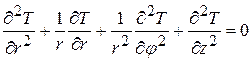Здесь Ñ - оператор Гамильтона (набла)

.

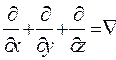Оператор Лапласа:

.

.

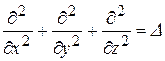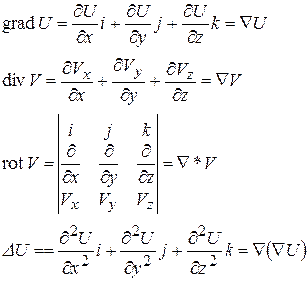Лекция № 2 Условия однозначности для процессов

Теплопроводности

Так как дифференциальное уравнение теплопроводности выведено на основе общих законов физики, то оно описывает явление теплопроводности в самом общем виде. То есть это уравнение описывает целый класс явлений теплопроводности. Чтобы из бесчисленного количества выделить конкретно рассматриваемый процесс и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса – условия однозначности или краевые условия.