Звукоизоляция однородного ограждения. Закон массы

Два способа снижения уровня проникающего в помещение внешнего шума

Внешний шум, проникающий вовнутрь закрытого помещения, а также «собственный» шум от источников внутри помещения можно уменьшить частично, применяя звукопоглощающие материалы и конструкции различного типа, то есть средствами звукопоглощения.

Практика и расчеты показывают, что только средствами звукопоглощения снизить уровень шума можно не более чем на 12÷15 дБ и то лишь в области дальнего звукового поля (в области преимущественно отраженной звуковой энергии); в ближнем же звуковом поле (вблизи источников шума) это снижение еще меньше.

Сделаем оценочный расчет.

Пусть общая площадь ограждений помещения равна S,а средний коэффициент звукопоглощения до их облицовки специальными звукопоглощающими материалами (усредненный по материалам и по частотам) равен α_ср. Тогда эквивалентная площадь звукопоглощения cоставит А₀ = α_ср∙S.

Теперь предположим, что все поверхности ограждений облицованы «идеальным» звукопоглотителем, у которого α =1 (на всех частотах). В этом идеализированном случае ЭПЗ помещения станет максимальной и равной А = α∙S = S.Тогда максимальное снижение уровня шума в помещении за счет облицовки ограждений ЗПМ составит

ΔL_max = 10∙lg (A/A₀ ) = 10∙lg (1/ α_ср).

Для обычных строительных материалов (бетон, кирпич, дерево, линолеум и т.п.) средний коэффициент звукопоглощения (по материалам и по частотам) можно взять близким к величине α_ср≈ 0,03.

Тогда ΔL_max ≤10∙lg (1/0,03) ≈ 10∙lg 33 ≈ 15 дБ.

Эта оценочная цифра ставит предел эффективности использования ЗПМ и ЗПК для снижения уровня шума в помещении.

Более эффективным способом снижения уровня внешнего шума, проникающего внутрь помещения через ограждение, является использование его звукоизолирующих свойств.

Звукоизоляция однородного ограждения. Закон массы

Под однородным ограждением понимают не только однослойную плиту (стену), сделанную из одного определенного материала, но и слоистые конструкции из разных материалов, если они жестко сцеплены между собою на границах. Так, кирпичную или бетонную стену, оштукатуренную с одной или обеих сторон, можно считать однородным ограждением.

С другой стороны, эту стену с гипсокартонной плитой на относе (если в зазоре между ними воздух или пористый материал) нельзя отнести к однородному ограждению.

Далее, для простоты, однородное ограждение будем рассматривать как бесконечно протяженный плоский слой материала небольшой (много меньше длины звуковой волны λ) толщины δ, который характеризуется средней объемной плотностью ρ (средним объемным весом γ = g∙ρ) и средней поверхностной массой m_п.

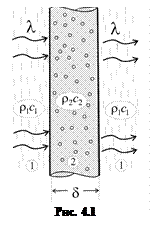
Наиболее простые соотношения получаются при нормальном падении звуковой волны на плиту, когда с обеих сторон она окружена одной и той же средою (рис. 4.1). Если речь идет о звукоизоляции воздушного шума, то такой средою является воздух.

Теория дает следующий результат для звукоизолирующей способности такой плиты-ограждения:

R =10∙lg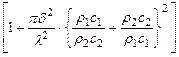 ,(4.1)

где δ – толщина плиты; λ – длина звуковой волны; ρ₁с₁ и ρ₂с₂ – акустические сопротивления сред.

Видно, что звукоизоляция плиты ограждения в значительной степени определяется соотношением между акустическими сопротивлениями ограждения и окружающей

его среды.

В частности, для целей звукоизоляции от воздушного шума нет особого смысла использовать пористо-волокнистые материалы, так как их акустические сопротивления не столь уж сильно отличаются от воздуха, так что получить заметную звукоизоляцию можно лишь при очень толстом слое материала. На низких частотах эта толщина может составить несколько метров!

Из вышеприведенной формулы (4.1) для звукоизоляции однородного ограждения вытекают два важных случая, часто встречающихся на практике.

Первый из них имеет место, когда акустическое сопротивление плиты-ограждения во много раз больше, чем у окружающей среды (как правило, воздуха), то есть ρ₂с₂ >> ρ₁с₁.В частности, для бетона ρ₂с₂ ≈10⁷, а для воздуха ρ₁с₁ (ρ₀с₀ ) ≈410 Па∙с/м. Тогда в формуле (4.1) отношением ρ₁с₁ / ρ₂с₂ можно пренебречь и она примет вид

R =10∙lg 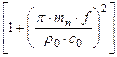,(4.2.)

где m_п =ρ₂ ∙δ – поверхностная масса плиты, то есть масса 1 м² плиты;

f =c/λ – частота звука; ρ₀с₀ – акустическое сопротивление воздуха.

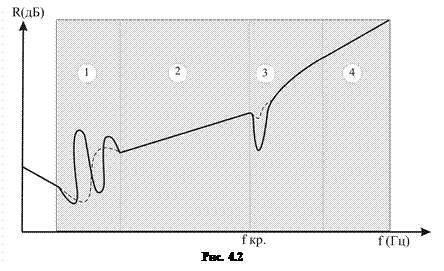
1 – область резонансов;

2 – область действия «закона массы», наклон 6дБ/окт;

3 – область «волновых совпадений»;

4 – продолжение области действия закона массы, наклон 7,5дБ/окт

­

Видно, что звукоизоляция растет как с увеличением частоты звука, так и с увеличением поверхностной массы плиты-ограждения.

Вторая закономерность проявляется в том случае, когда средой, окружающей «ограждение», является не воздух, и акустическое сопротивление этой среды много больше, чем у «преграды», то есть выполняется обратное соотношение ρ₁с₁ >> ρ₂с₂. Например, между стальными переборками корабля (ρ₁с₁ ≈ 4∙10⁷) помещен слой губчатой резины (ρ₂с₂ ≈ 1,5∙10⁴). Здесь также проявляется эффект звукоизоляции структурного шума, и он тем выше, чем меньше жесткость (выше упругость) материала прокладки.

Возвратимся к формуле (4.2.) для звукоизолирующей способности однородного ограждения от воздушного шума. Если учесть, что в диффузном звуковом поле звуковые волны могут падать на ограждение по всевозможным направлениям (а не только нормально к поверхности) и провести усреднение по углам (от 0 до 90⁰), то выражение (4.2) для звукоизоляции можно привести к виду

R ≈ 20∙lg (m_п∙f ) – 47,5 (дБ) (4.3)

Примечание: В формуле (4.2) пренебрегают единицей, показатель степени «2» выносят перед знаком логарифма, а величина 20∙lg 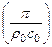(с учетом усреднения) дает число, близкое к «– 47,5».

В такой форме оно носит название «закона массы».

По существу он содержит два утверждения:

■ При всяком удвоении поверхностной массы однородного ограждения его звукоизоляция воздушного шума (на любой фиксированной частоте) увеличивается на 6 дБ.

■ При всяком удвоении частоты звука звукоизоляция однородного ограждения также увеличивается на 6 дБ.