Численное интегрирование
В прикладных исследованиях часто возникает необходимость вычисления определенных интегралов 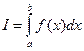 . К сожалению, в подавляющем большинстве случаев получить значение такого интеграла известными аналитическими методами не удается. Например, интеграл
. К сожалению, в подавляющем большинстве случаев получить значение такого интеграла известными аналитическими методами не удается. Например, интеграл 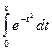 широко используется при исследовании процессов теплообмена и диффузии, в статистической физике и теории вероятностей. Однако его значение не может быть выражено в виде конечной комбинации элементарных функций. В других случаях окончательный результат выражается чрезмерно громоздкой формулой, неудобной для дальнейших вычислений. Иногда подынтегральная функция задана таблично, и точное значение интеграла получить невозможно. Тогда применяют специальные методы численного интегрирования.
широко используется при исследовании процессов теплообмена и диффузии, в статистической физике и теории вероятностей. Однако его значение не может быть выражено в виде конечной комбинации элементарных функций. В других случаях окончательный результат выражается чрезмерно громоздкой формулой, неудобной для дальнейших вычислений. Иногда подынтегральная функция задана таблично, и точное значение интеграла получить невозможно. Тогда применяют специальные методы численного интегрирования.
Определение: квадратурной формулойназывается приближенное равенство вида 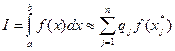 , (4.1)
, (4.1)
где 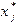 - некоторые точки из отрезка
- некоторые точки из отрезка 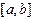 , называемые узлами, а
, называемые узлами, а 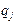 - числовые коэффициенты, называемые весами квадратурной формулы. Величина
- числовые коэффициенты, называемые весами квадратурной формулы. Величина 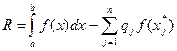 называется погрешностью (или остаточным членом) квадратурной формулы.
называется погрешностью (или остаточным членом) квадратурной формулы.
Ниже рассматриваются некоторые широко распространенные простые квадратурные формулы. Все они основаны на геометрических представлениях. Будем интерпретировать интеграл как площадь криволинейной трапеции, ограниченной графиком функции 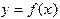 (при
(при 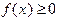 ), осью абсцисс и прямыми
), осью абсцисс и прямыми 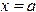 и
и 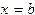 (рис.7).
(рис.7).
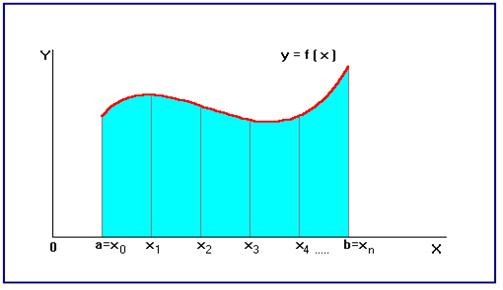
Рис.7
Разобьем отрезок 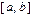 на элементарные отрезки
на элементарные отрезки 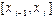 точками
точками 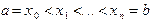 . Интеграл разобьется при этом на сумму элементарных интегралов
. Интеграл разобьется при этом на сумму элементарных интегралов 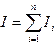 , где
, где 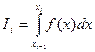 , что соответствует разбиению площади исходной криволинейной трапеции на сумму площадей элементарных криволинейных трапеций (рис.7). Введем обозначения:
, что соответствует разбиению площади исходной криволинейной трапеции на сумму площадей элементарных криволинейных трапеций (рис.7). Введем обозначения: 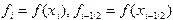 , где
, где 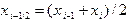 - середина элементарного отрезка. Для простоты шаг
- середина элементарного отрезка. Для простоты шаг 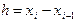 будем считать постоянным (
будем считать постоянным ( 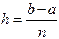 ).
).
Дата добавления: 2021-09-07; просмотров: 377;











