Для дифференциальных уравнений 1-го порядка
Обыкновенные дифференциальные уравнения довольно часто встречаются в различных прикладных задачах строительной механики, электротехники, исследовании разнообразных технологических процессов и поведения сложных инженерных систем. Характеристики соответствующих явлений, как правило, непрерывным образом зависят от времени и подчиняются физическим законам, которые формулируются в виде дифференциальных уравнений с начальными условиями, то есть требуют решения задачи Коши. Подавляющее большинство возникающих на практике задач такого рода невозможно решить без использования вычислительной техники. Поэтому численные методы решения задачи Коши играют в инженерных и научно-технических расчетах особую роль.
Рассмотрим дифференциальное уравнение первого порядка, разрешенное относительно производной с начальным условием в точке 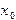 :
:
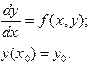 (5.1)
(5.1)
Из теории дифференциальных уравнений известно, что если 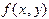 и
и 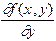 непрерывны в окрестности точки
непрерывны в окрестности точки 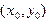 , то в этой окрестности существует, и единственное, решение задачи Коши (5.1).
, то в этой окрестности существует, и единственное, решение задачи Коши (5.1).
На первом этапе численного решения отрезок 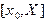 области непрерывного изменения аргумента заменяется набором дискретных точек
области непрерывного изменения аргумента заменяется набором дискретных точек 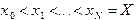 , который называется сеткой. Сами точки
, который называется сеткой. Сами точки 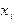 называются узлами сетки, а величина
называются узлами сетки, а величина 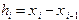 - шагом сетки. Мы будем рассматривать такие сетки, у которых шаг постоянен, тогда
- шагом сетки. Мы будем рассматривать такие сетки, у которых шаг постоянен, тогда
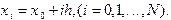 (5.2)
(5.2)
Следующий этап в построении численного метода состоит в замене задачи Коши ее дискретным аналогом - системой уравнений, решая которую можно последовательно найти значения 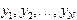 сеточной функции
сеточной функции 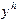 , играющие роль приближений к значениям решения задачи Коши в узлах сетки.
, играющие роль приближений к значениям решения задачи Коши в узлах сетки.
Метод Эйлера
Простейший дискретный аналог дифференциального уравнения (5.1) представляет собой уравнение
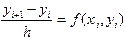 ,
,
приводящее к методу Эйлера. Вычисление очередного значения 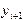 осуществляется здесь по формуле
осуществляется здесь по формуле
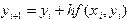 . (5.3)
. (5.3)
Геометрическая интерпретация метода Эйлера проиллюстрирована на рис.12. На каждом шаге вычислений строится касательная к интегральной кривой в точке 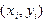 , и за
, и за 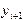 принимается ордината точки ее пересечения с
принимается ордината точки ее пересечения с
вертикальной прямой 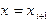 . В результате неизвестная интегральная кривая заменяется ломаной линией, называемой ломаной Эйлера.
. В результате неизвестная интегральная кривая заменяется ломаной линией, называемой ломаной Эйлера.
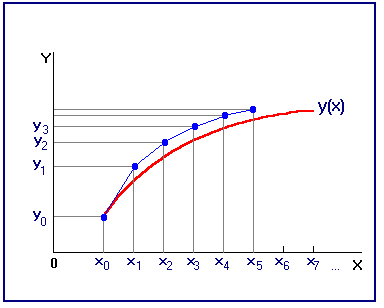
Рис. 12
Реализация численного алгоритма на компьютере предполагает построение алгоритма, позволяющего вычислить решение поставленной дискретной задачи Коши. В данном случае (и во всех ниже рассматриваемых случаях) вычисления производятся по явной формуле - значение сеточной функции зависит только от предыдущих значений, и программирование алгоритма не вызовет особых затруднений. Такие методы называют явными. В неявных методах правая часть уравнения может зависеть от 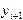 , и на каждом шаге возникает необходимость решения некоторого уравнения относительно
, и на каждом шаге возникает необходимость решения некоторого уравнения относительно 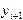 . Примером здесь может служить неявный метод Эйлера, когда вычисления производят по формуле
. Примером здесь может служить неявный метод Эйлера, когда вычисления производят по формуле 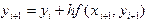 .
.
Дата добавления: 2021-09-07; просмотров: 412;











