Интегрирование по частям
Интегральное исчисление функции одной Переменной
Неопределенный интеграл. Основные понятия и свойства
Неопределенным интегралом от функции 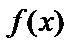 называется выражение вида
называется выражение вида 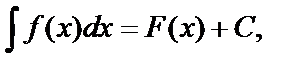 если
если 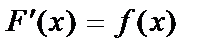 . Функция
. Функция 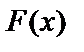 называется первообразной для заданной функции
называется первообразной для заданной функции 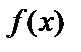 .
.
Свойства неопределенного интеграла:
1. 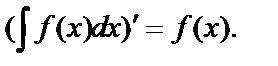
2. 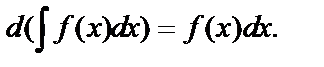
3. 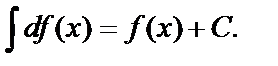
4. 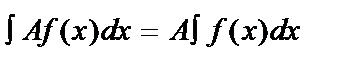 , где A ≠ 0.
, где A ≠ 0.
5. 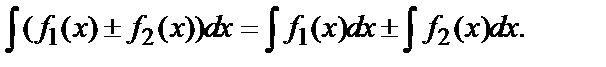
6.2 Таблица основных неопределенных интегралов
1. 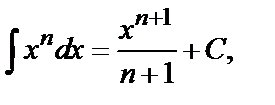 где
где 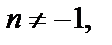 (
( 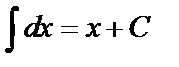 ).
).
2. 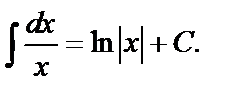
3. 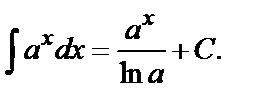
4. 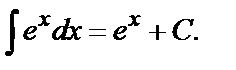
5. 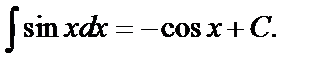
6. 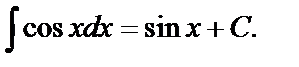
7. 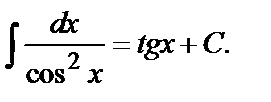
8. 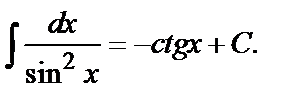
9. 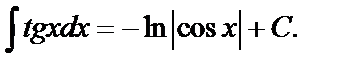
10. 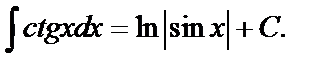
11. 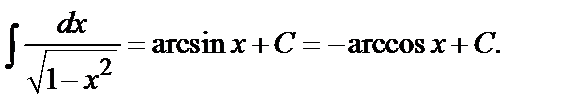
12. 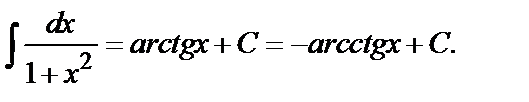
13. 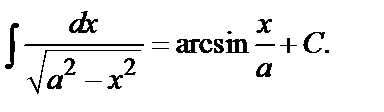
14. 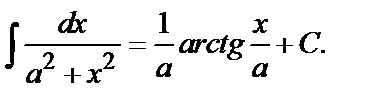
15. 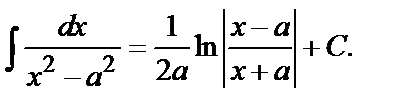
16. 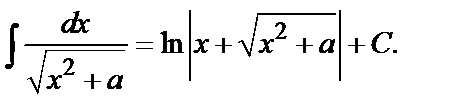
Основные методы интегрирования
Интегрирование способом подстановки
В основе интегрирования способом подстановки (или замены переменной) лежит свойство инвариантности формул интегрирования, которое заключается в следующем: если 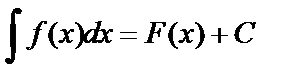 , то
, то 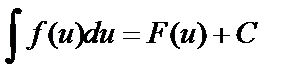 , где
, где 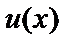 - произвольная дифференцируемая функция от x.
- произвольная дифференцируемая функция от x.
Замена переменной в неопределенном интеграле производится с помощью подстановки: 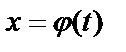 , где t – новая переменная, а
, где t – новая переменная, а 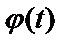 – непрерывно дифференцируемая функция. В этом случае формула замены переменной:
– непрерывно дифференцируемая функция. В этом случае формула замены переменной:
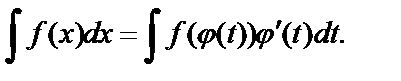 (6.1)
(6.1)
Функцию 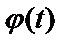 стараются выбирать таким образом, чтобы правая часть формулы приобрела более удобный для интегрирования вид.
стараются выбирать таким образом, чтобы правая часть формулы приобрела более удобный для интегрирования вид.
Интегрирование по частям
Интегрирование по частям называется нахождение интеграла по формуле:
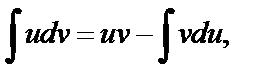 (6.2)
(6.2)
где u и v – непрерывно дифференцируемые функции от x. С помощью формулы (6.2) отыскание интеграла 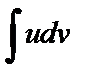 сводится к нахождению другого интеграла
сводится к нахождению другого интеграла 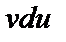 ; ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
; ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
При этом в качестве u берется функция, которая при дифференцировании упрощается, а в качестве v – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Так, при нахождении интегралов вида
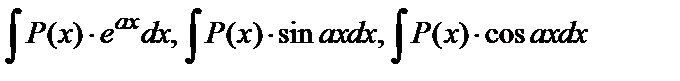
за u следует принять многочлен P(x), а за dv - соответственно выражения 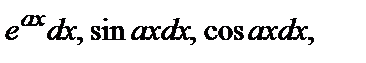 при отыскании интегралов вида
при отыскании интегралов вида 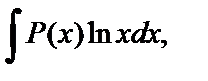
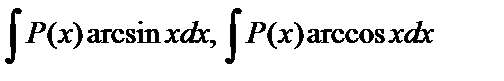 за u принимаются соответственно функции
за u принимаются соответственно функции 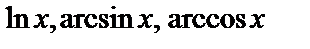 , а за dv – выражение
, а за dv – выражение 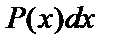 .
.
Дата добавления: 2018-11-26; просмотров: 1056;











