Интегрирование оригинала

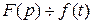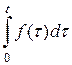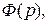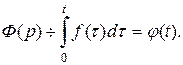Пусть .Каково изображение ? Обозначим его через т.е. Продифференцируем .

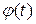Пусть 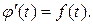Но 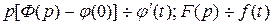, поэтому 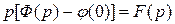. Остаётся 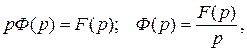при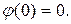

Итак, 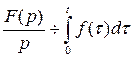, т.е. при интегрировании оригинала от нуля до t изображение делится на p.

Найдем изображение для неопределенного интеграла (первообразной) 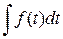= 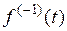. Определенный интеграл 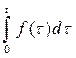также является первообразной для функции , поэтому 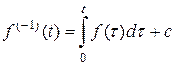.Положив 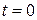, получим .

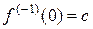Тогда 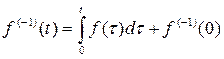, где 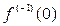– постоянная.

Изображение функции 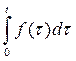найдено ранее, поэтому

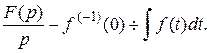
Дифференцирование изображения

Пусть 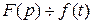, т.е. 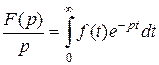.(2.3)

Продифференцируем обе части равенства (2.3) по параметру p.

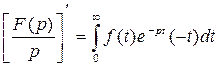, или 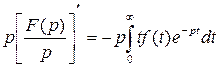. Тогда

.

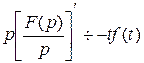Продифференцируем обе части равенства (3.1) дважды по параметру p.

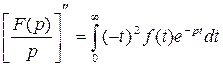, или .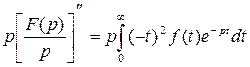

Следовательно,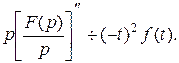

Продифференцировав равенство (3.1)по параметру p n раз, получим:

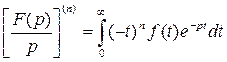, или

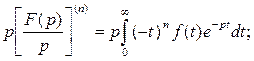
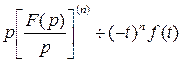, где 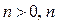– целое.

Изучим поведение интеграла Лапласа при .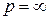

Теорема 2.3

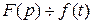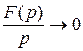Если – функция с ограниченным ростом, , то при .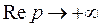

Доказательство

Пусть 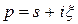, тогда .

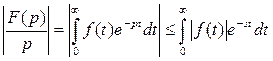Рассмотрим сколь угодно малое 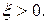Покажем, что можно указать такое p, с достаточно большой вещественной частью 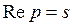, для которого

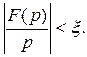В равенстве для 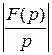разобьём интеграл, стоящий справа, на два интеграла:

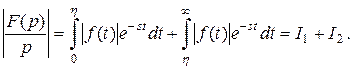
Рассмотрим 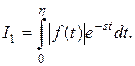Так как 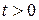, то для тех p, для которых 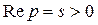, 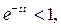следовательно, 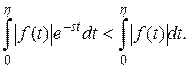Подберём 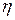так, чтобы интеграл 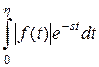был меньше 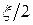. Это возможно, потому что функция непрерывна или кусочно-непрерывна пр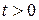и и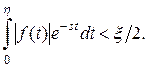

Рассмотрим 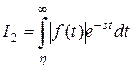, где – функция с ограниченным ростом, 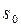– показатель роста. Рассмотрим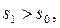 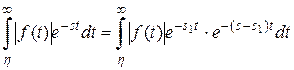. Функция 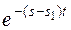при 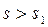, наибольшее значение на промежутке 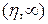имеет при 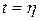. Интеграл 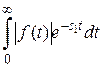сходится, т.к. – функция с ограниченным ростом, а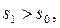

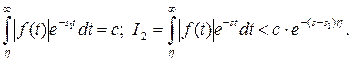
Здесь c, s₁ и 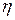-фиксированные величины, а переменная s произвольная. Взяв 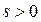и достаточно большим, получим: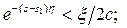 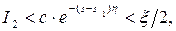т.к. 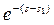- убывающая функция аргумента s.

Итак, при достаточно больших 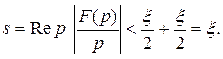Рассуждения справедливы для любых 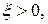сколь угодно малых. Следовательно, выполняется неравенство: 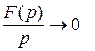при .

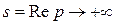Теорема смещения