Интегрирование комплексных функций
Возможны разные подходы к определению понятия интеграла от комплексной функции. Так, например, 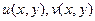 - функции двух переменных, тогда можно вычислять двойные интегралы от них по некоторой плоской области, и объединять результаты в комплексное число вида
- функции двух переменных, тогда можно вычислять двойные интегралы от них по некоторой плоской области, и объединять результаты в комплексное число вида 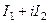 . Однако в качестве основного всё же исторически был принят метод интегрирования по кривой, именно при таком подходе возможно введение понятия первообразной
. Однако в качестве основного всё же исторически был принят метод интегрирования по кривой, именно при таком подходе возможно введение понятия первообразной 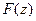 , а также получают применение многие факты из теории векторного поля. Итак, определение интеграла и метод его вычисления:
, а также получают применение многие факты из теории векторного поля. Итак, определение интеграла и метод его вычисления:
Определение. Пусть в области 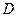 задана некоторая функция
задана некоторая функция 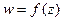 (не обязательно аналитическая), и в области
(не обязательно аналитическая), и в области 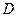 расположена кусочно-гладкая кривая
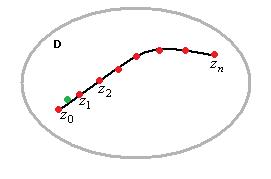
расположена кусочно-гладкая кривая 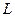 (не обязательно замкнутая). Введём разбиение кривой на n частей с помощью (n-1) внутренних точек. Таким образом, получилась последовательность точек
(не обязательно замкнутая). Введём разбиение кривой на n частей с помощью (n-1) внутренних точек. Таким образом, получилась последовательность точек 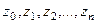 , расположенных по порядку на кривой, где
, расположенных по порядку на кривой, где 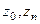 - начальная и конечная точки. Обозначим
- начальная и конечная точки. Обозначим 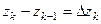 . Выберем на каждом участке дуги какую-то точку
. Выберем на каждом участке дуги какую-то точку 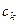 и составим интегральную сумму:
и составим интегральную сумму: 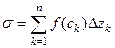 . Предел интегральных сумм при измельчении разбиения, т.е. при
. Предел интегральных сумм при измельчении разбиения, т.е. при 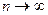 , называется интегралом от функции
, называется интегралом от функции 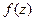 по кривой
по кривой 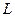 и обозначается
и обозначается 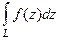 .
.
Метод вычисления.При вычислении необходимо разбить на действительную и мнимую части как функцию, так и дифференциал, затем раскрыть скобки и получить 4 слагаемых. Но их можно объединить по два, в двух из них нет мнимой единицы, а в двух она есть:
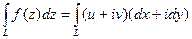 =
= 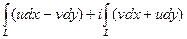 .
.
Таким образом, при вычислении всё сводится к двум криволинейным интегралам 2-го рода от векторных полей 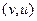 и
и 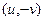 , а мнимая единица умножается на второй из них, при этом в самих вычислениях она фактически не участвует.
, а мнимая единица умножается на второй из них, при этом в самих вычислениях она фактически не участвует.
Дата добавления: 2020-03-17; просмотров: 859;











