Интегрирование дифференциальных уравнений движения голономной системы.

Пусть координата 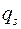есть циклическая координата, то есть она не содержится в функции Лагранжа:

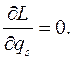
Из уравнения Лагранжа для циклической координаты имеем

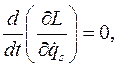
Откуда циклический обобщенный импульс постоянен на движении системы:

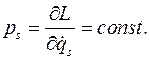
то есть 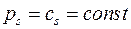постоянен на решениях уравнений Лагранжа.

Функция 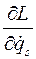называется циклическиминтегралом уравнений Лагранжа. Обычно пишут:

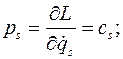
Интеграл энергии консервативной системы.

Введем функцию

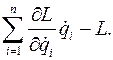
Покажем, что для консервативной системы эта функция есть первый интеграл уравнений Лагранжа. Для этого посчитаем полную производную по времени от введенной функции: 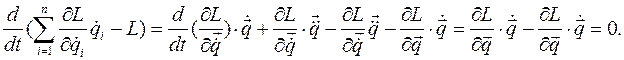Покажем, однако, что

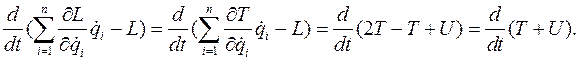
Значит, 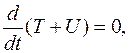откуда следует, что в консервативной системе механическая энергия, в силу уравнений движения, постоянна на решениях:

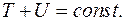
Этот первый интеграл уравнений движения называется интеграл энергии.

Преобразование Лежандра.

Рассмотрим выпуклую функцию 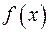, для которой 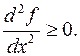Зададим скаляр p. Построим функцию

.

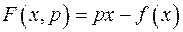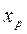Найдем, при каком значении эта функция максимальна. Это будет там, где

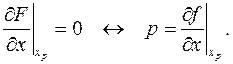
Построим теперь функцию

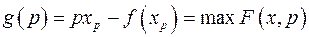
для некоторого множества значений параметра р. При этом соответствующие значения 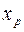ищем из условия

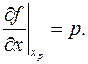
Определение. Преобразованием Лежандра функции 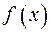называется функция

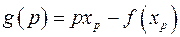
нового переменного р, причем точку 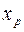, где кривая 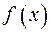дальше всего отстоит от прямой y = px , ищут для каждого р из условия:

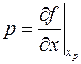
Пример.

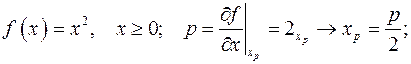
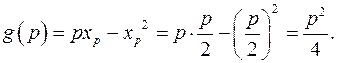
Определение выше обобщается на выпуклые (вогнутые) скалярные функциивекторногоаргумента ;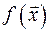

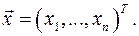
Тогда

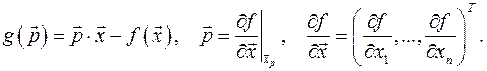
Свойства преобразования Лежандра.

1. Если при преобразовании Лежандра 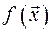переходит в 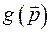, то повторное преобразование Лежандра функции 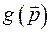снова переходит в функцию :

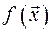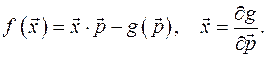
2. Если функция 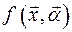зависит еще и от параметра 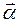, то