Принцип наименьших квадратов

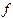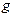В отличие от задач интерполяции, аппроксимация по методу наименьших квадратов не требует выполнения условия (3.2) совпадения функций и в узловых точках. Такая задача возникает в самых различных областях науки и техники, например, при обработке экспериментальных данных.

Пусть функция 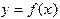задана таблицей приближенных значений:

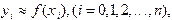(3.3) полученных из эксперимента с ошибками 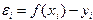. Такие ошибки могут носить случайный характер и зачастую уровень погрешности бывает значительным (на рис.6,б показан пример графика ”истинной” функции 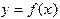вместе с точками 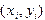- данными эксперимента).

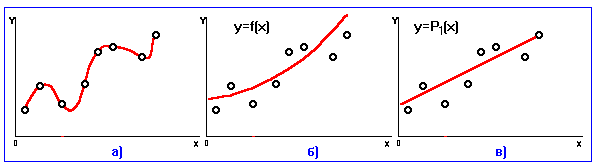
Рис.6

Предположим, что для аппроксимации функции используется многочлен 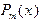степени 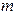. Если применять метод интерполяции, то тогда необходимо, чтобы выполнялось условие 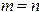. В этом случае график функции пройдет точно через точки 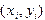(смотри рис.6,а), однако при интерполировании происходит повторение ошибок наблюдений, в то время, как при обработке результатов эксперимента желательно, напротив, их сглаживание. Кроме того, при очень большом значении 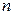степень многочлена слишком велика, а это может привести к значительным вычислительным погрешностям.

Пусть 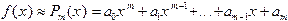. Из различных критериев, позволяющих выбрать параметры 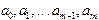так, чтобы приближенное равенство удовлетворялось наилучшим образом, наиболее часто используют принцип наименьших квадратов. Согласно этому критерию параметры выбирают так, чтобы минимизировать величину

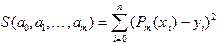. (3.4)

Эта величина, как видно из формулы, представляет собой сумму квадратов отклонений аппроксимирующего многочлена от табличных значений. Как известно из курса дифференциального исчисления, такая функция многих переменных в точке экстремума (минимума) должна иметь частные производные по всем переменным, равные нулю:

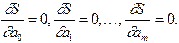(3.5)