Формулы прямоугольников

Заменим приближенно площадь элементарной криволинейной трапеции площадью прямоугольника, основанием которого является отрезок 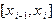, а высота равна либо 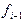(рис.8,а), либо 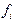(рис.8,б), либо 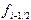(рис.8,в).

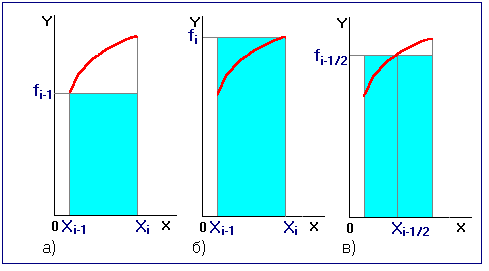
Рис.8

Если взять за высоту прямоугольника значение 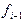, то , то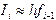гда, суммируя все элементарные площади, получаем квадратурную формулу левых прямоугольников:

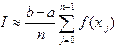. (4.2)

Во втором случае 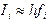, и тогда приходим к квадратурной формуле правых прямоугольников:

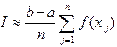. (4.3)

Наконец, если за высоту прямоугольника брать значение функции 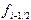в средней точке , то 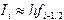, а составная формула выглядит как

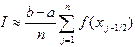. (4.4)

Названия формул (4.2) и (4.3) следуют из геометрической иллюстрации (рис.8). В соответствии с этим приближенное равенство (4.4) иногда называют формулой центральных прямоугольников. Ниже, когда будут рассматриваться вопросы о точности квадратурных формул, выяснится, что она точнее на порядок по сравнению с (4.2) и (4.3). По этой причине для численного интегрирования гораздо чаще применяют (4.4) и называют ее просто формулой прямоугольников. Для всех трех полученных формул их применение означает приближенную замену площади исходной криволинейной трапеции площадью ступенчатой фигуры, состоящей из элементарных прямоугольников (рис.9 - для формулы центральных прямоугольников).

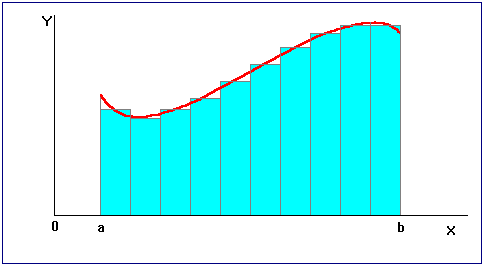
Рис.9

Формула трапеций

Соединив отрезком точк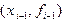и и 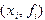на графике функции 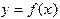, получим трапецию (рис.10). Заменим теперь приближенно площадь элементарной криволинейной трапеции площадью построенной трапеции. Тогда получим элементарную квадратурную формулу трапеций 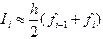. Пользуясь этой формулой для каждой элементарной трапеции и суммируя их площади, получим составную квадратурную формулу трапеций:

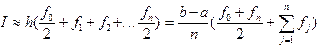. (4.5)

Эта формула соответствует приближенной замене площади исходной криволинейной трапеции площадью фигуры, ограниченной ломаной линией, проходящей через точки .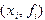

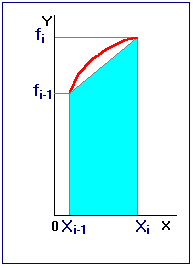
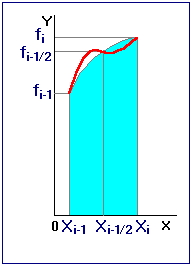
Рис. 10 Рис. 11