Формула Симпсона (парабол)

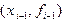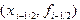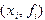Если площадь элементарной криволинейной трапеции заменить площадью фигуры, расположенной под параболой, проходящей через точки , и , то получим приближенное равенство 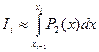. Здесь 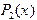- интерполяционный многочлен 2-й степени с узлами 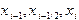. На рис.11 показана такая парабола, а график функции 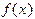на элементарном отрезке для большей наглядности изображен искривленным. Если построить интерполяционный многочлен по указанным трем точкам, он будет выражаться формулой

.

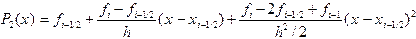Интегрирование полученного выражения на элементарном отрезке приводит к равенству

.

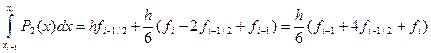Таким образом, получена элементарная квадратурная формула Симпсона. Применяя эту формулу и суммируя результаты для всего отрезка интегрирования, выводим составную квадратурную формулу Симпсона:

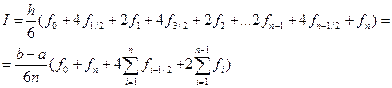(4.6)

Замечание 1. Учитывая геометрическую интерпретацию формулы Симпсона, ее иногда называют формулой парабол.

Замечание 2.В случае, когда число элементарных отрезков разбиения четно ( 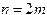), в формуле Симпсона можно использовать узлы лишь с целыми индексами:

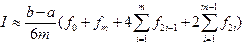(4.7)

Эта формула легко вытекает из (4.6), если при выводе принять 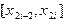за элементарный отрезок длины .

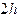Оценка погрешности

Итак, полученные формулы (4.2)-(4.7) позволяют приближенно вычислять определенные интегралы. Программирование здесь сводится к тривиальному использованию операторов цикла для вычисления сумм, поэтому нет необходимости приводить здесь тексты программ. Другой важный вопрос - в каких случаях применять ту или иную формулу - связан с погрешностью вычислений.

Оценим погрешность выведенных квадратурных формул. Будем использовать обозначение 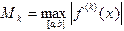- максимальное значение производной 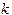-го порядка от подынтегральной функции на отрезке 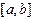. Выведем сначала оценку погрешности для формулы (4.2). Представим ее остаточный член в виде:

.

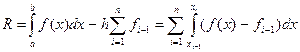Пусть функция 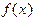непрерывно дифференцируема. Тогда, используя формулу Тейлора 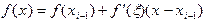, где 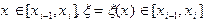, имеем 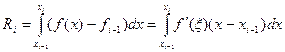, и тогда

.

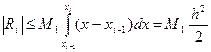Так как 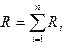, то, заменяя 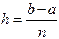, приходим к оценке погрешности:

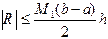. (4.8)

В точности такая же оценка погрешности справедлива и для формулы правых прямоугольников. Ее можно получить, проведя аналогичные выкладки при разложении функции по формуле Тейлора в окрестности точки .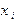

Подобным же способом оцениваются погрешности других квадратурных формул. Справедливы следующие утверждения (без доказательства):

Пусть функция 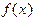дважды непрерывно дифференцируема на отрезке интегрирования. Тогда для составной квадратурной формулы прямоугольников (центральных) справедлива оценка погрешности:

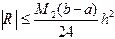, (4.9)

а для формулы трапеций:

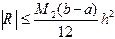. (4.10)

Приведенные оценки показывают, что формулы (4.2) и (4.3) имеют лишь первый порядок точности относительно 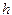, поэтому они используются крайне редко. Предпочтительнее использование формул (4.4) и (4.5), которые имеют второй порядок точности. Однако вычисление интегралов по формуле Симпсона дает четвертый порядок точности относительно 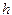(для функции 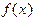здесь требуется существование непрерывной производной четвертого порядка):

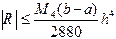. (4.11)

Замечание3. Из оценок (4.9)-(4.11) следует, что формулы прямоугольников и трапеций точны для многочленов первой степени, а формула Симпсона - для многочленов четвертой степени.

Замечание4. При вычислении интегралов по приведенным выше квадратурным формулам необходимо учитывать тот фактор, что при увеличении числа узлов возрастает влияние ошибок округления, поэтому для повышения точности рекомендуется не столько увеличивать это число, сколько применять более точную формулу.