Интегрирование по методу Симпсона.

Пусть n = 2m − чётное число, а у_i = f(x_i) (i = 0..n) − значения функции у = f(x) для равноотстоящих точек a = x₀, x₁, x₂, …, x_n = b с шагом h =(b-a)/n = (b-a)/2m. На паре участков (рис.3) кривая у = f(x) заменяется параболой у = L(x), коэффициенты которой подобраны так, что она проходит через точки у₀, у₁, у₂.

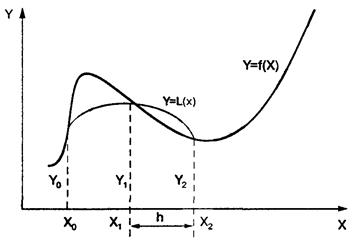
Рис.3 Геометрическая интерпретация интегрирования по методу Симпсона.

Площадь криволинейной трапеции, ограниченной сверху параболой, составит:

.

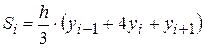Суммируя площади всех криволинейных трапеций, получим:

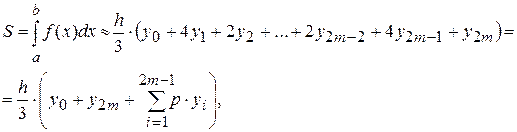
Где p = 6-p, p = 4. Следовательно, формула Симпсонадля численного интегрирования имеет вид:

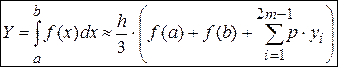(9)

Остаточный член имеет вид: 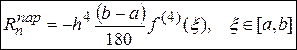(10)

На практике для оценки абсолютной погрешности 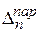формулы Симпсона применяют следующие соотношения:

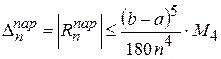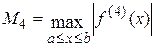1. , (11)

При этом, как правило, получают для 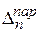завышенную оценку.

2. Правило Рунге (n − чётное) даёт более тонкую оценку :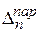

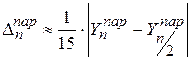(12)

Но при этом может получиться для 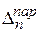заниженная оценка, чего следует опасаться.

Формулы прямоугольников и трапеций дают точное значение интеграла, когда подынтегральная функция f(x) линейна, ибо тогда f ″(x) = 0, а формула Симпсона является точной для многочленов до третьей степени, т. к. в этом случае f ⁽⁴⁾ = 0.

Если функция у = f(x) задана таблично и её производные найти затруднительно, то в предполо- жении отсутствия быстро колеблющихся составляющих можно применить приближённые формулы для погрешностей, выраженные через конечные разности:

(*)

(**)

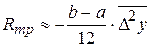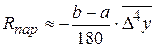Выбор шага

1. Пусть требуется вычислить интеграл с точностью ε. Используя формулу соответствующего остаточного члена R, выбирают h таким образом, чтобы выполнялось неравенство .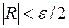

2. Двойной пересчёт. ( Правило Рунге).

Лекция 4

ЧИСЛЕННОЕ РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ И НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

Если алгебраическое или трансцендентное уравнение достаточно сложное, то его корни сравнительно редко удаётся найти точно. Поэтому большое значение приобретают способы приближённого нахождения корней уравнения и оценки степени их точности.

Процесс нахождения приближённых значений корней уравнения:

f(x) = 0, (1)

где функция f(x) определена и непрерывна в некотором конечном или

бесконечном интервале a < x < b разбивается на два этапа: 1) отделение корней; 2) уточнение корней до заданной степени точности.

Отделение корней.

Всякое значение λ, обращающее функцию f(x) в нуль, т. е. такое, что f(λ) = 0, называется корнем уравнения (1) или нулём функции f(x).

Отделить корни − это значит разбить всю область допустимых значений на отрезки, в каждом из которых содержится один корень. Отделение корней можно произвести двумя способами − графическим и аналитическим.

Графический метод отделения корней: a) строят график функции у = f(x) для уравнения вида f(x) = 0. Значения действительных корней уравнения являются абсциссы точек пересечения графика функции у = f(x) с осью Ох (рис.1);

b) представляют уравнение (1) в виде φ(х) = g(x) и строят графики функций

у = φ(х) и у = g(x). Значения действительных корней уравнения являются абсциссы точек пересечения графиков функций у = φ(х) и у = g(x) (рис.2).

Отрезки, в которых заключено только по одному корню, легко находятся.

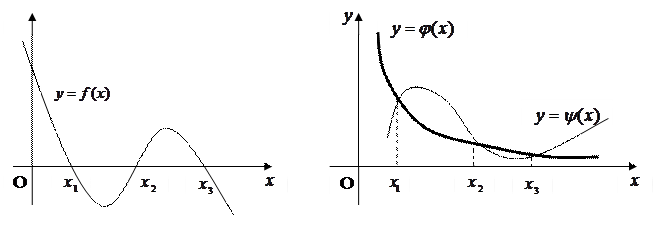
Рис.1. Рис.2.

Аналитический метод отделения корней основан на следующей теореме:

если непрерывная на отрезке 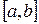функция 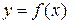принимает на концах отрезка значения разных знаков, т.е. 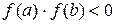, то внутри этого отрезка находится хотя бы один корень уравнения 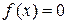; если при этом

производная 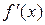сохраняет знак внутри отрезка 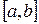, то корень является единственным.