Интегрирование по множеству бесконечной меры

Пусть (X,S,m) – пространство с σ-конечной мерой. В силу определения σ-конечности существует неубывающая последовательность измеримых множеств 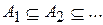, для которых 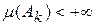для всех k и .

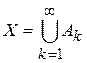Введём сначала понятие интеграла Лебега по множеству бесконечной меры в случае неотрицательной функции.

Пусть 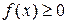на X и f – измеримая. Поскольку все 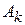– измеримы, то имеют смысл и конечны 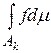, причём 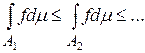, поэтому существует предел .

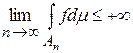Пусть 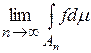существует и конечен, тогда функция f называется интегрируемой по Лебегу на множестве с σ-конечной мерой и .

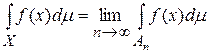Данное определение корректно и не зависит от выбора расширяющейся системы .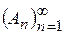

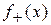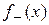Пусть теперь f – измеримая функция произвольного знака. Рассмотрим функции и , тогда 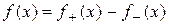, 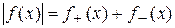. Функция f называется интегрируемой по Лебегу на X, если на X интегрируемы обе функци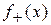и и 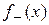. При этом, по определению .

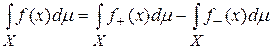Нетрудно показать, что для интегрируемости измеримой функции f необходимо и достаточно, чтобы 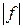была интегрируема.

Множество X с σ-конечной мерой 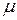может быть представлено в виде счётного объединения попарно непересекающихся множеств 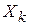, т.е. 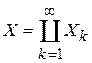, 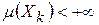. В этом случае измеримая функция f называется интегрируемой на X, если сходится ряд 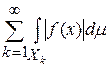. Интегралом Лебега интегрируемой функции f называется число .

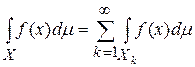Все свойства, установленные для интегралов Лебега по множеству конечной меры, остаются справедливыми и по множеству σ-конечной меры, включая теоремы о предельном переходе.