Метод Эйлера с уточнением
Приближенное решение задачи Коши методом Эйлера характеризуется очень медленной сходимостью (его погрешность убывает пропорционально лишь первой степени  ). Это является серьезным препятствием для использования его на практике. Однако расчетные формулы можно подправить, чтобы увеличить точность вычислений. Рассмотрим следующую модификацию метода Эйлера. На первом этапе по формуле (5.3) вычисляется начальное приближение к
). Это является серьезным препятствием для использования его на практике. Однако расчетные формулы можно подправить, чтобы увеличить точность вычислений. Рассмотрим следующую модификацию метода Эйлера. На первом этапе по формуле (5.3) вычисляется начальное приближение к 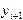 , а затем корректируется по формулам:
, а затем корректируется по формулам:
 (5.4)
(5.4)
Метод приближенного решения задачи Коши по формулам (5.4) относится к методам класса прогноз-коррекция и иногда его называют методом Эйлера-Коши. Геометрическая иллюстрация этого метода представлена на рис.13. Если принять ломаную Эйлера в виде цепочки векторов, то значение сеточной функции по формулам (5.4) можно представить как полусумму двух последующих звеньев-векторов.
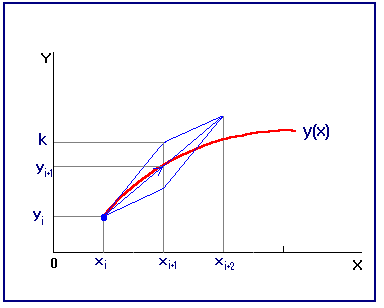
Рис.13
Как видно из рисунка, вычисленное значение гораздо находится ближе к графику искомой функции. Метод Эйлера-Коши имеет второй порядок точности, и доказательство этого факта можно найти в [1].
Методы Рунге-Кутты
Наиболее популярными среди классических явных одношаговых методов являются методы Рунге-Кутты. Рассмотренные выше методы можно рассматривать как частные случаи этого класса методов. Самым известным из методов Рунге-Кутты является метод четвертого порядка точности. Вычисления на каждом шаге здесь проводятся последовательно в четыре этапа. Сначала вычисляются вспомогательные коэффициенты, а затем они подставляются в основную формулу:
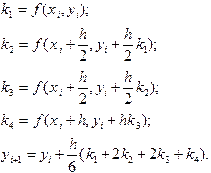 (5.5)
(5.5)
Этот метод весьма прост и, как показывает практика, довольно эффективен в обычных расчетах.
Литература
- Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. - М., Высшая школа, 1994.
Приложение: Варианты контрольных работ.
Вариант № 1
1. Методом половинного деления и методом хорд определить один из корней уравнения 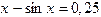 с точностью до e=0,0001
с точностью до e=0,0001
2. Методом Гаусса найти решение системы уравнений:
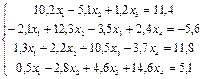
3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию: 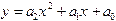
| x | -2 | -1 | |||
| y | 24,43 | 12,86 | 7,02 | 7,74 | 14,60 |
4. Методами трапеций и Симпсона вычислить интеграл и сделать проверку: 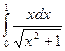
5. Используя метод Эйлера 1ого порядка, составить таблицу решения дифференциального уравнения  с начальным условием
с начальным условием  и шагом
и шагом 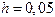 на отрезке
на отрезке 
Вариант № 2
1. Методом половинного деления и методом касательных определить один из корней уравнения  с точностью до e=0,0001
с точностью до e=0,0001
2. Методом простых итераций найти решение системы уравнений с точностью e=0,00001:

3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию: 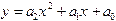
| x | -3 | -2 | -1 | ||
| y | 5,24 | 8,42 | 9,51 | 8,21 | -6,62 |
4. Методами модиф. прямоугольников и трапеций вычислить интеграл и сделать проверку: 
5. Используя метод Эйлера-Коши, составить таблицу решения дифференциального уравнения 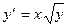 с начальным условием
с начальным условием  и шагом
и шагом  на отрезке
на отрезке 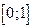
Вариант № 3
1. Методом половинного деления и методом простых итераций определить один из корней уравнения  с точностью до e=0,0001
с точностью до e=0,0001
2. Методом Зейделя найти решение системы уравнений с точностью e=0,00001:

3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию: 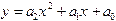
| x | -2 | -1 | |||
| y | 32,61 | 12,43 | 1,25 | 0,09 | 8,74 |
4. Методами “правых” прямоугольников и Симпсона вычислить интеграл и сделать проверку: 
5. Используя метод Рунге-Кутта, составить таблицу решения дифференциального уравнения  с начальным условием
с начальным условием 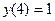 и шагом
и шагом 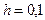 на отрезке
на отрезке 
Вариант № 4
1. Методом половинного деления и методом хорд определить один из корней уравнения 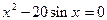 с точностью до e=0,00001
с точностью до e=0,00001
2. Методом простых итераций найти решение системы уравнений с точностью e=0,00001:
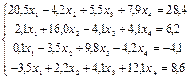
3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию: 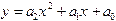
| x | -2 | -1,5 | -1 | ||
| y | -0,03 | -3,31 | -5,08 | -6,15 | -3,27 |
4. Методами трапеций и “левых” прямоугольников вычислить интеграл и сделать проверку: 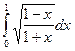
5. Используя метод Эйлера-Коши, составить таблицу решения дифференциального уравнения 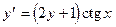 с начальным условием
с начальным условием 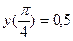 и шагом
и шагом 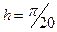 на отрезке
на отрезке 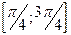
Вариант № 5
1. Методом половинного деления и методом касательных определить один из корней уравнения  с точностью до e=0,0001
с точностью до e=0,0001
2. Методом Гаусса найти решение системы уравнений :

3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию: 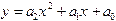
| x | |||||
| y | 0,08 | -7,93 | -12,14 | -12,09 | -8,12 |
4. Методами Симпсона и трапеций вычислить интеграл и сделать проверку:

5. Используя метод Рунге-Кутта, составить таблицу решения дифференциального уравнения  с начальным условием
с начальным условием  и шагом
и шагом  на отрезке
на отрезке 
Вариант № 6
1. Методом половинного деления и методом простых итераций определить один из корней уравнения  с точностью до e=0,0001
с точностью до e=0,0001
2. Методом Зейделя найти решение системы уравнений с точностью e=0,00001:
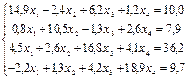
3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию: 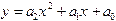
| x | -2 | -1 | |||
| y | 5,95 | -3,12 | -5,98 | -2,87 | 6,05 |
4. Методами “левых” прямоугольников и Симпсона вычислить интеграл и сделать проверку: 
5. Используя метод Эйлера 1ого порядка, составить таблицу решения дифференциального уравнения 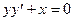 с начальным условием
с начальным условием  и шагом
и шагом  на отрезке
на отрезке 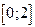
Вариант № 7
1. Методом половинного деления и методом простых итераций определить один из корней уравнения  с точностью до e=0,00001
с точностью до e=0,00001
2. Методом Гаусса найти решение системы уравнений :

3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию: 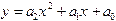
| x | -1 | 0,5 | |||
| y | -15,31 | -6,84 | -5,26 | -5,34 | -9,81 |
4. Методами трапеций и Симпсона вычислить интеграл и сделать проверку: 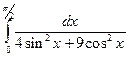
5. Используя метод Эйлера-Коши, составить таблицу решения дифференциального уравнения 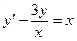 с начальным условием
с начальным условием 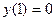 и шагом
и шагом 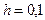 на отрезке
на отрезке 
Вариант № 8
1. Методом половинного деления и методом касательных определить один из корней уравнения 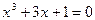 с точностью до e=0,0001
с точностью до e=0,0001
2. Методом Гаусса найти решение системы уравнений :
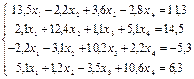
3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию: 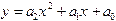
| x | -1 | ||||
| y | 6,54 | 3,71 | 2,58 | 3,58 | 6,69 |
4. Методами Симпсона и трапеций вычислить интеграл и сделать проверку: 
5. Используя метод Рунге-Кутта, составить таблицу решения дифференциального уравнения 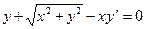 с начальным условием
с начальным условием 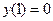 и шагом
и шагом  на отрезке
на отрезке 
Вариант № 9
1. Методом половинного деления и методом простых итераций определить один из корней уравнения  с точностью до e=0,0001
с точностью до e=0,0001
2. Методом Зейделя найти решение системы уравнений с точностью e=0,00001:
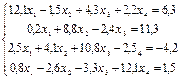
3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию: 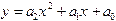
| x | |||||
| y | -10,47 | -7,29 | -6,52 | -7,36 | -11,02 |
4. Методами “левых” прямоугольников и Симпсона вычислить интеграл и сделать проверку: 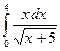
5. Используя метод Эйлера 1ого порядка, составить таблицу решения дифференциального уравнения 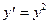 с начальным условием
с начальным условием  и шагом
и шагом 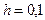 на отрезке
на отрезке 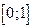
Вариант № 10
1. Методом половинного деления и методом хорд определить один из корней уравнения  с точностью до e=0,00001
с точностью до e=0,00001
2. Методом простых итераций найти решение системы уравнений с точностью e=0,00001:
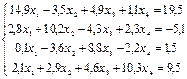
3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию: 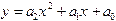
| x | -2 | -1 | |||
| y | 15,76 | 6,88 | 1,67 | 0,96 | 3,57 |
4. Методами трапеций и “левых” прямоугольников вычислить интеграл и сделать проверку: 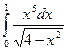
5. Используя метод Эйлера-Коши, составить таблицу решения дифференциального уравнения  с начальным условием
с начальным условием  и шагом
и шагом 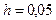 на отрезке
на отрезке 
Дата добавления: 2021-09-07; просмотров: 539;











