Квадратичная аппроксимация

Аналогично решается задача нахождения коэффициентов аппроксимирующего многочлена 2-го порядка. В этом случае он имеет вид 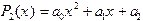и график представляет собой параболу. Минимизируемая функция - функция трех переменных 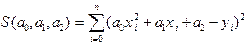. Повторяя те же выкладки, что и в предыдущем разделе, можно прийти к системе трех уравнений с тремя неизвестными (проделайте их самостоятельно):

,

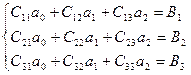где , , , ,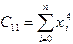

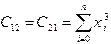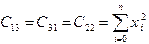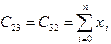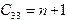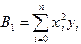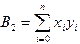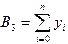, , , . (3.8)

Как видно из формул (3.8), полученная система симметрична и хорошо решается методом Гаусса, не требуя выбора главных элементов. Однако для многочленов более высокой степени ( 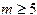) использование такого метода не рекомендуется, так как вычисленные на ЭВМ параметры могут оказаться полностью искаженными ошибками округления.

Замечание 1. В том случае, когда m=n, найденный методом наименьших квадратов аппроксимирующий многочлен совпадает с интерполяционным многочленом. При этом минимизируемая функция 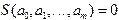, и значения многочлена в узловых точках совпадают с табличными значениями.

Замечание 2. Как правило, при использовании метода наименьших квадратов предполагается, что 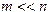. В этом случае метод обладает некоторыми сглаживающими свойствами.