Численное интегрирование.
Определённый интеграл
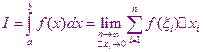 где,
где,
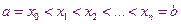
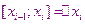
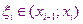
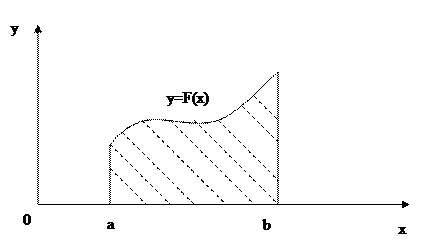
Часто возникает задача численного интегрирования, например в таких случаях когда:
1)аналитически, через элементарные функции интеграл не берётся;
2)численное интегрирование необходимо использовать, если подинтегральная функция задана в табличном виде.
При численном интегрировании используется определение интеграла и его геометрического смысла. Приближенное значение интеграла мы получим, если в интегральной сумме ограничимся конечным числом слагаемых.
Метод 21
Метод прямоугольников.
Простейшим методом численного интегрирования является метод прямоугольников. В этом методе интеграл вычисляется с помощью усеченной интегральной суммы, а в качестве точки 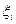
берётся середина отрезка 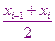 . При вычислении можно использовать правую или левую сторону этого отрезка
. При вычислении можно использовать правую или левую сторону этого отрезка 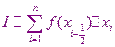
Метод 22
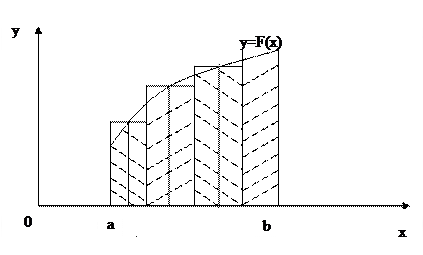
Метод трапеции
В этом методе интеграл, приближенно заменяется на сумму площадей трапеций, образующихся после замены графика функции 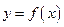 ломаной, соединяющей точки
ломаной, соединяющей точки 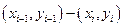 .
.
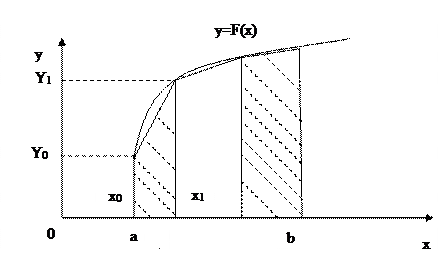
Площадь трапеции с номером 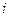 равняется
равняется
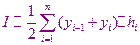
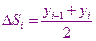
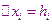 -шаг интегрирования
-шаг интегрирования
Для практического использования важен случай интегрирования с постоянным шагом 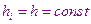 тогда
тогда 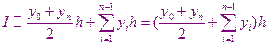
Погрешность интегрирования определяется шагом разбиения h. С уменьшением h точность возрастает. Точность вычисления интеграла по методу прямоугольников и трапеций имеет порядок 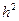 .
.
При интегрировании методом прямоугольников подинтегральная функция на каждом частном отрезке 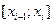 апроксимируется постоянной величиной равной
апроксимируется постоянной величиной равной 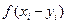
А в методе трапеций подинтегральная функция апроксимируется линейной зависимостью, проходящей через точку 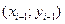 ,
, 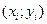 . Существуют методы, для которых подинтегральная функция апроксимируется другими зависимостями.
. Существуют методы, для которых подинтегральная функция апроксимируется другими зависимостями.
Метод 23
Метод Симпсона.
Подинтегральное выражение апроксимируется квадратичной зависимостью вида 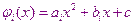
Для применения метода Симпсона отрезок интегрирования 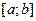 разбиваем на четное число 2n частных отрезков с одинаковым шагом
разбиваем на четное число 2n частных отрезков с одинаковым шагом 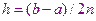 , а в качестве аппроксимирующей функции берём полином Лагранжа, проходящий через три точки:
, а в качестве аппроксимирующей функции берём полином Лагранжа, проходящий через три точки: 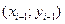 ,
, 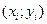 ,
, 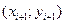 .
.
Можно показать, что интеграл от соответствующего полинома Лагранжа
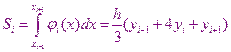

Таким образом 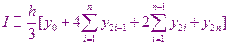
Погрешность метода Симпсона пропорциональна 0( 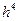 )-и имеет порядок
)-и имеет порядок 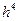 .
.
Метод 24
Метод Гаусса.
В предыдущих методах при численном интегрировании подинтегральную функцию вычисляют в равноотстоящих друг от друга узлах. В методе Гаусса для повышения точности численного интегрирования значения подинтегральной функции вычисляют в специально подобранных узлах.
Рассмотрим сначала стандартный отрезок 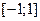 и зададим число m= числу узлов, в которых вычисляется подинтегральная функция. Координаты этих узлов обозначим
и зададим число m= числу узлов, в которых вычисляется подинтегральная функция. Координаты этих узлов обозначим
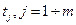
и получим для определённого интеграла приближенное выражение
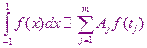 (1.1)
(1.1)
Узлы 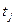 подбирают таким образом, чтобы обеспечить максимальную точность выражения (1.1).
подбирают таким образом, чтобы обеспечить максимальную точность выражения (1.1).
Она будет максимальной в том случае, если узлы 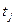 будут соответствовать корням полиномов Лагранжа.
будут соответствовать корням полиномов Лагранжа.
Метод Гаусса представляет собой группу методов различающихся числом узлов. Значения параметров 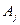 ,
, 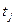 для m=2;3 запишем в таблицу.
для m=2;3 запишем в таблицу.
| m | j | 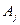
| 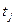
| №метода |
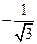
| ||||
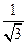
| ||||
| 0,7745967 | 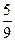
| |||
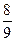
| ||||
| 0,7745967 | 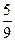
|
С помощью формулы Гаусса (1.1) с m-узлами на стандартном отрезке 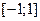 можно получить формулу для вычисления интеграла на произвольном отрезке
можно получить формулу для вычисления интеграла на произвольном отрезке 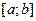 .
.
Для этого разбиваем отрезок 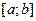 на n равных частичных отрезков. На каждом отрезке
на n равных частичных отрезков. На каждом отрезке 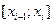
Задаём m узлов с помощью формулы
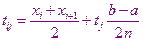
i – это номер частичного отрезка;
j – это номер узла в каждом частичном отрезке.
Для
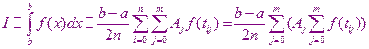
Метод 24 даёт точные значения интеграла для полиномов степени 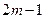 , при m=2 метод Симпсона и метод Гаусса имеют приблизительно одинаковую точность. Однако метод Симпсона более удобен, так как для него узлы расположены равномерно, поэтому метод Гаусса целесообразно использовать при m>2.
, при m=2 метод Симпсона и метод Гаусса имеют приблизительно одинаковую точность. Однако метод Симпсона более удобен, так как для него узлы расположены равномерно, поэтому метод Гаусса целесообразно использовать при m>2.
Метод 26
Метод Монте-Карло.
Во многих задачах исходные данные носят случайный характер. Для решения таких задач применяется статистико-вероятностный подход. На основе такого подхода разработан метод статистических испытаний, называемый также методом Монте-Карло. В методе Монте-Карло для случайной величины X с определённым законом распределения находится математическое ожидание, 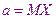 причем в качестве приблизительного значения математического ожидания можно использовать среднее значение из серии испытаний случайной величины X.
причем в качестве приблизительного значения математического ожидания можно использовать среднее значение из серии испытаний случайной величины X.
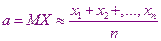
Это соотношение можно использовать для приближенного вычисления интеграла. Пусть Т – это случайная величина равномерно распределённая на отрезке 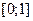 . Равномерность распределения означает, что плотность распределения этой случайной величины во всех точках отрезка
. Равномерность распределения означает, что плотность распределения этой случайной величины во всех точках отрезка 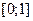 имеет одинаковое значение равное единице. То есть плотность распределения для этой случайной величины равна
имеет одинаковое значение равное единице. То есть плотность распределения для этой случайной величины равна
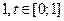
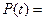
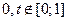
В компьютерах встроены генераторы случайных чисел, имеющие нормальное распределение. Для вычисления 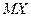 по определению математического ожидания используется следующая формула
по определению математического ожидания используется следующая формула
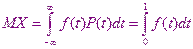
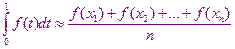
где, 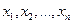 - это случайные числа равномерно распределённые на
- это случайные числа равномерно распределённые на 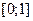 .
.
Тогда 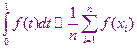
При вычислении интеграла на 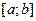 путем замены
путем замены 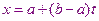 интеграл приводится к отрезку
интеграл приводится к отрезку 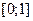 если отрезок
если отрезок 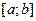 разбить на n частей, и каждый отрезок преобразовать в единичный, то для интеграла по
разбить на n частей, и каждый отрезок преобразовать в единичный, то для интеграла по 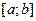
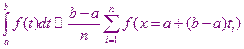 где
где 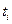 - это случайное число на
- это случайное число на 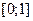 .
.
Метод 27
Дата добавления: 2017-03-12; просмотров: 2807;











