Лекция 7. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ

План

7.1 Метод Эйлера

7.2. Метод Рунге-Кутта

В инженерной практике довольно часто приходится встречаться с обыкновенными дифференциальными уравнениями при решении различных прикладных задач. Обыкновенным дифференциальным уравнением называется выражение вида:

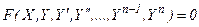, (7.1)

где 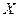- независимая переменная; 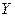- искомая функция от 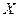; 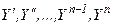- производные порядка .

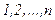Порядок старшей производной, входящей в уравнение (7.1), называется порядком дифференциального уравнения.

Простейшим обыкновенным дифференциальным уравнением является уравнение 1-го порядка

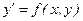. (7.2)

Основная задача, относящаяся к этому уравнению, есть задача Коши: найти решение дифференциального уравнения (7.2) в виде 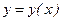, удовлетворяющее начальному условию 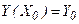, т.е. требуется найти интегральную кривую 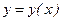, проходящую через заданную точку .

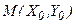Для нахождения решения дифференциального уравнения (7.1) необходимо задать такое количество начальных условий, какое соответствует порядку старшей производной, а именно задать значения:

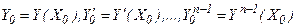(7.3)

Уравнение (7.1) называется разрешенным относительно старшей производной, если оно имеет вид:

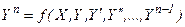(7.4)

Если дифференциальное уравнение (7.1) разрешимо относительно старшей производной, то его можно свести к системе обыкновенных дифференциальных уравнений 1-го порядка заменой на неизвестную функцию 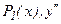на 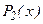и т.д.

Таким образом, имеем

,

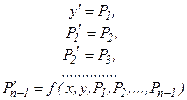причем

.

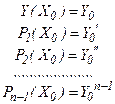При решении инженерных задач чаще всего приходится иметь дело с уравнениями, общее решение которых не выражается в аналитическом виде. Поэтому возникает необходимость применять те или иные методы, дающие приближенное решение задачи.

Метод Эйлера

Метод численного решения дифференциального уравнения 1-го порядка

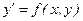(7.5)

с начальным условием 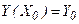основан на разложении решения в ряд Тейлора в 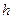-окрестности точки :

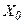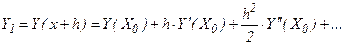
При отбрасывании всех членов ряда, содержащих производные 2-го и высших порядков, получим

,

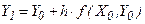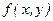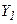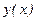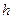где - правая часть уравнения (7.5). Пользуясь значением из разложения в –окрестности точки 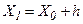, получим 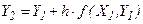, аналогично продолжая для следующей 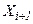точки, получим

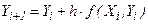. (7.6)

Если дано уравнение 2-го порядка

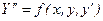(7.7)

c начальными условиям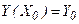и и 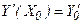, то такое уравнение можно свести к системе двух уравнений 1-го порядка

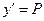(7.8)

,

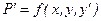причем

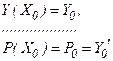. (7.9)

Тогда приближенные значения функци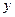й и 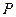в точке можно вычислить

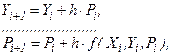(7.10)

где 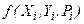- правая часть уравнения (7.7).

При достаточно малой величине шага 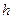метод Эйлера дает решение с большой точностью, т.к. погрешность решения близка к .

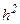Разновидностью рассмотренного выше метода Эйлера, известного в литературе также как метод Эйлера-Коши, является метод Эйлера-Коши с итерациями. Он заключается в вычислении на каждом шаге начального значения

.

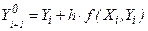Затем с помощью итерационной формулы

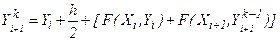
решение уточняется. Итерации проводят до тех пор, пока совпадает заданное число цифр результата на двух последних шагах итераций. Погрешность метода составляет примерно 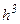. Обычно число итераций не должно превышать 3-4, иначе нужно уменьшить шаг .

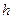Модифицированный метод Эйлера второго порядкареализуется следующими рекуррентными формулами:

,

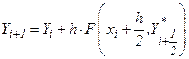где 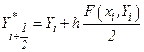. Метод дает погрешность порядка 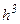и имеет меньшее время вычислений, поскольку вместо нескольких итераций производится вычисление только одного значения .

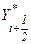Метод трапеций – одна из модификаций метода Эйлера второго порядка. Он реализуется применением на каждом шаге формулы

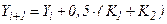
где 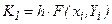; 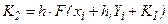и дает погрешность порядка 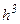. Этот метод относится к общим методам Рунге-Кутта.

Метод Рунге-Кутта

Метод Рунге-Кутта является наиболее распространенным методом решения дифференциальных уравнений при постоянном заданном шаге. Его достоинством является высокая точ­ность.

Алгоритм реализации метода Рунге-Кутта для уравнений 1-го порядка (типа (7.7)) заключается в циклических вычислениях 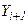на каждом 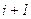шаге по следующим формулам:

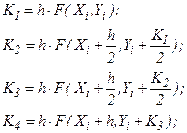
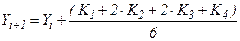(7.11)

Для дифференциальных уравнений 2-го порядка (типа (7.9)) метод реализуется с помощью следующих формул:

;

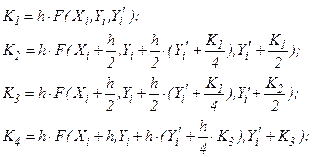
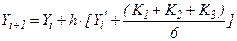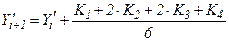(7.12)

Перед началом вычислений надо задать шаг 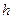и начальные условия (7.3).

Контрольные вопросы

1. Что такое численное дифференцирование?

2. Суть метода Эйлера и оценка его погрешности?

3. Какие бывают разновидности метода Эйлера?

4. Оценка погрешности в методе Эйлера-Коши с итерациями?

5. Оценка погрешности модифицированного метода Эйлера 2-го порядка?

6. Метод трапеций и оценка его погрешности?

7. Суть метода Рунге-Кутта?

8. Алгоритм метода Рунге-Кутта для уравнения 1-го порядка?

9. Алгоритм метода Рунге-Кутта для дифференциального уравнения 2-го порядка?