Численное дифференцирование.
Напомним, что производной функции y=f(x) называется предел отношения приращения функции ∆y к приращению аргумента Δx при стремление Δx к нулю
y`= f `(x)= 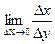 ∆y= f(x +Δx )- f(x) (1)
∆y= f(x +Δx )- f(x) (1)
В численных расчетах на ЭВМ, когда функция задана таблицей значений, значение шага Δx полагают равному конечному числу и для вычисления значений производных получают приближенное равенство
y`≈ 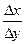 (2)
(2)
Это соотношение называется аппроксимацией производных с помощью отношения конечных разностей (т.к. ∆y и Δx конечные в отличие от значений в формуле (1)).
Рассмотрим аппроксимацию производной для функции y=f(x), заданной в табличной форме xi= x0, x1… xn yi= y0, y1… yn
Пусть шаг разности между соседними значениями аргумента постоянен и равен h. Запишем выражение в точке x=x1
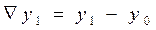 ∆x=h
∆x=h
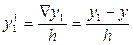 (3)
(3)

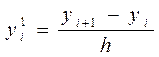 ~0(h)
~0(h)
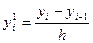 ~0(h)
~0(h)
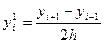 ~0(h2)
~0(h2)
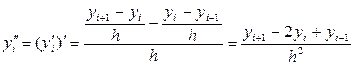 ~0(h2)
~0(h2)
Можно найти производные с помощью формул Тейлора
f(x +Δx )= f(x)+ 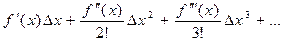

(1) y(xi-1 )=y(xi –h) = y(x)- hf `(xi )+0(h2)
yi-1= yi- hf `(xi )+0(h2)
y`(xi)=f `(xi)= 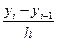 ~0(h)
~0(h)
(2) y(xi+1 )=y(xi +h) = y(x)+ hf `(xi )+0(h2)
yi+1=yi+ hf `(xi )+
y`(xi)=f `(xi)= 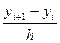 ~0(h)
~0(h)
(1) y(xi-1 )=yi –h yi `+ 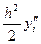 + 0(h3)
+ 0(h3)
(2) y(xi+1 )=yi +h yi `+ 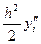 + 0(h3)
+ 0(h3)
(1)+ (2)
yi-1+ yi+1=2 + 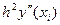
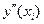 =
=  ~0(h2)
~0(h2)
(2)- (1)
yi+1 -yi-1 =2hyi `
yi `= 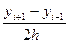 ~0(h2)
~0(h2)
Можно использовать полиномы Лагранжа и Ньютона.
Метод неопределенных коэффициентов.
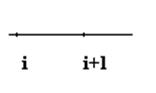
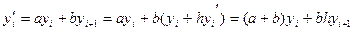
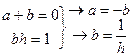
a=-b=- 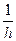
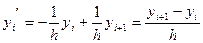
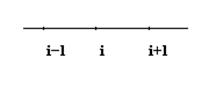

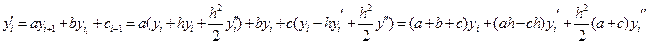
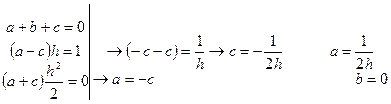
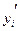 =
= 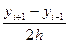
И так далее.
Лекция 5
Дата добавления: 2016-07-27; просмотров: 2463;











