Численное дифференцирование

Основные вопросы, рассматриваемые на лекции:

1. Постановка задачи численного дифференцирования

2. Численное дифференцирование на основе интерполяционных формул Ньютона

3. Оценка погрешности дифференцирования с помощью многочлена Ньютона

4. Численное дифференцирование на основе интерполяционной формулы Лагранжа

5. Оценка погрешности численного дифференцирования с помощью многочлена Лагранжа

1. Постановка задачи численного дифференцирования

Функция y = f(x) задана таблицей:

на отрезке [a; b] в узлах a = x₀ < x₁ < x₂ < : <x_n =b</x_. Требуется найти приближенное значение производной этой функции в некоторой точке х* 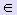[a; b]. При этом х* может быть как узловой точкой, так и расположенной между узлами.

· Численное дифференцирование на основе интерполяционных формул Ньютона

Считая узлы таблицы равноотстоящими, построим интерполяционный полином Ньютона. Затем продифференцируем его, полагая, что f '(x) φ'(x) на [a; b]:

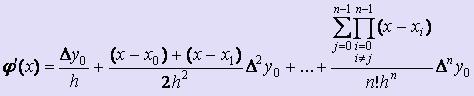₍₁₎
Формула значительно упрощается, если производная ищется в одном из узлов таблицы:х* = xi = x0 + ih:
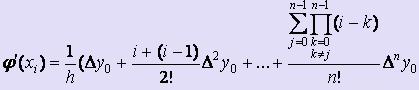₍₂₎
Подобным путём можно получить и производные функции f (x) более высоких порядков. Однако, каждый раз вычисляя значение производной функции f (x) в фиксированной точке х в качестве х0 следует брать ближайшее слева узловое значение аргумента.

· Численное дифференцирование на основе интерполяционной формулы Лагранжа

Запишем формулу Лагранжа для равноотстоящих узлов в более удобном виде для дифференцирования:

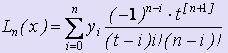
Затем, дифференцируя по х как функцию от t, получим:

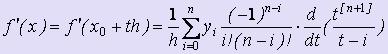
Пользуясь этой формулой можно вычислять приближённые значения производной таблично-заданной функции f (x) в одном из равноотстоящих узлов.
Аналогично могут быть найдены значения производных функции f(x) более высоких порядков.