Метод Рунге-Кутта для ОДУ высших порядков.
Метод Рунге – Кутта можно использовать для решения дифференциальных уравнений высокого порядка (второго или более высокого). Для этого дифференциальное уравнение сводится к системе уравнений первого порядка.
Например: дифференциальное уравнение второго порядка:
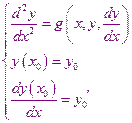
Введём переменную 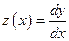 , в результате решаемая задача приводится к следующей задаче:
, в результате решаемая задача приводится к следующей задаче:
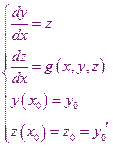 получили систему двух уравнений первого порядка.
получили систему двух уравнений первого порядка.
Метод 33
Метод стрельбы.
Методы решения задачи Коши могут быть использованы при решении краевых задач. В качестве примера рассмотрим один из методов решения краевой задачи для дифференциального уравнения второго порядка, который называется методом стрельбы.
Решается дифференциальное уравнение второго порядка:
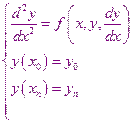
Заменим эту краевую задачу задачей Коши
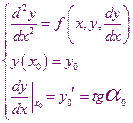
Задача сводится к тому, чтобы найти такой угол  , чтобы в точке
, чтобы в точке 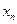 решение равнялось
решение равнялось 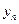 .
.
Эта задача зависит от угла 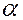 , как от параметра:
, как от параметра:
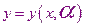
И нужно чтобы
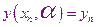
Решение этого уравнения есть  . Найдя,
. Найдя,  мы тем самым решим задачу как методом Коши.
мы тем самым решим задачу как методом Коши.

Метод 34
Дата добавления: 2017-03-12; просмотров: 2431;











