Графическое и численное дифференцирование.

Графическое дифференцирование начинают с построения графика функции по заданным значениям. При экспериментальном исследовании такой график получают с помощью самопишущих приборов. Далее проводят касательные к кривой в фиксированных положениях и вычисляют значения производной по тангенсу угла, образованного касательной с осью абсцисс.

На рис. 5.8, а изображена кривая 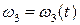полученная экспериментально на установке (рис. 5.6). Определение углового ускорения (искомой функции) проводят графическим дифференцированием по соотношению:

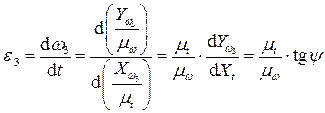(5.19)

Тангенс угла 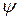наклона касательной к кривой 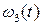в некоторой точке i представляют в виде отношения отрезков 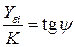, где К – выбранный отрезок интегрирования (рис. 5.8, б)

После подстановки этого соотношения в соотношение (5.19) полу­чают

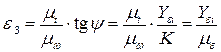
где 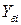- ордината искового графика углового ускорения;

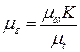
— масштаб искомого графика 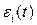; единицы СИ:[ 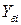] = мм; [ 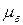] = мм/(рад 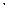с^-2).

График функции 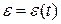строят по найденным значениям орди­нат для ряда позиций. Точки на кривой соединяют от руки плавной линией, а затем обводят с помощью лекала.

Графическое дифференцирование рассмотренным методом каса­тельных имеет относительно низкую точность. Более высокую точность получают при графическом диф­ференцировании методом хорд (рис. 5.8, в и г).

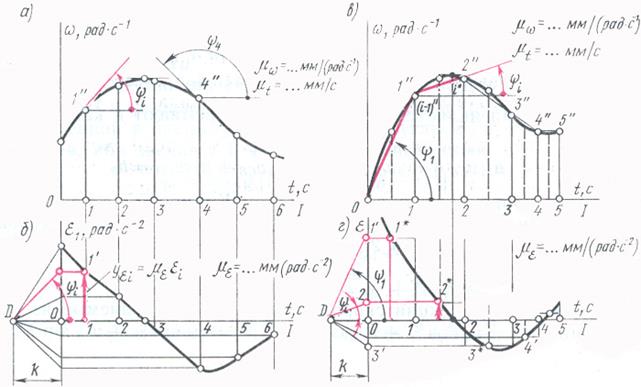На заданной кривой отмечают ряд точек 1", 2", 3", которые соединяют хордами, т.е. заменяют заданную кривую ломаной ли­нией. Принимают следующее, допущение: угол наклона касательных в точках, расположенных посередине каждого участка кривой, ра­вен углу 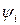наклона соответствующей хорды. Это допущение вносит некоторую погрешность, но она относится только к данной точке. Эти погрешности не суммируются, что обеспечивает приемлемую точность метода.

Рис (5.8)

Остальные построения аналогичны ранее описанным при графи­ческом дифференцировании методом касательных. Выбирают отре­зок 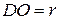(мм); проводят лучи, наклоненные под углами 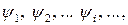до пересечения с осью ординат в точках 1', 2', 3' ... , которые переносят на ординаты, проведенные в середине каждого из интервалов. Полученные точки 1*, 2*, 3* являются точками иско­мой функции .

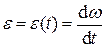Масштабы по осям координат при этом методе построения свя­заны таким же соотношением (5.21), которое было выведено для случая графического дифференцирования методом касательных.

Дифференцирование функции f(x), заданной (либо вычисленной) в виде массива чисел, выполняют методом численного дифферен­цирования с применением ЭВМ.

Чем меньше шаг 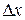в массиве чисел, тем точнее можно вычис­лить значение производной функции в этом интервале

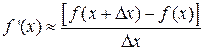
Можно пользоваться также выражением

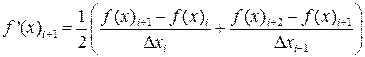
При численном дифференцировании используют интерполяцион­ные формулы, которые сопоставляют заданные значения какой-либо величины с функцией известного .класса, зависящей от не­скольких параметров, выбранную так, чтобы при заданных значе­ниях аргумента (в узлах интерполяции) значения функции совпа­дали с заданными значениями величины, т. е. чтобы график функ­ции проходил через заданные точки. Численное дифференцирование чувствительно к ошибкам, вызванным неточностью исходных дан­ных. Для функции у(х), заданной таблицей разностей для равно­отстоящих значений аргумента с шагом 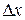, используют следующие соотношения для вычисления аргумента и производных:

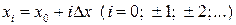
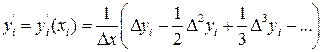
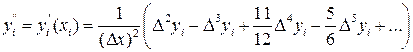
При разработке прикладных программ для численного дифференцирования на ЭВМ используют интерполяционные формулы Стирлинга, Бесселя, Ньютона и др.