Метод Рунге – Кутта.
Это метод, который позволяет учесть в ряде Тейлора члены, содержащие старшие производные.
Для этого при вычислении старших производных используется результаты расчетов в точках внутри интервала. Метод Рунге – Кутта объединяет целое семейство методов решения дифференциальных уравнений первого порядка. Отличаются эти методы порядком точности, т.е. числом слагаемых в ряде Тейлора.
Наиболее распространенным является метод, при котором удерживаются члены пропорциональные 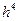 (метод 4-го порядка точности) когда говорят метод Рунге-Кутта, то имеют в виду метод четвёртого порядка.
(метод 4-го порядка точности) когда говорят метод Рунге-Кутта, то имеют в виду метод четвёртого порядка.
Расчеты в этом методе производятся по следующим формулам
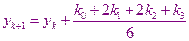
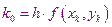
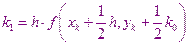
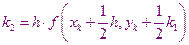
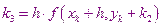
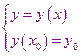

Метод 31
Метод Рунге-Кутта для решения систем ОДУ
Метод Рунге – Кутта может применяться для решения систем дифференциальных уравнений первого порядка. Например: при решении системы
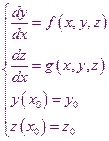 найдем
найдем 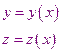
В этом случае расчеты производятся по следующим формулам:
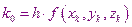
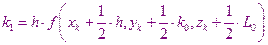
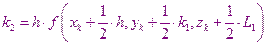
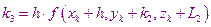
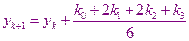
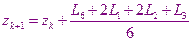
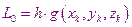
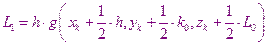
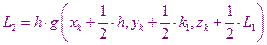
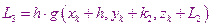
Метод 32
Дата добавления: 2017-03-12; просмотров: 1633;











