Метод возмущения параметров.

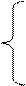Нам дана система

…………………..

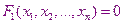
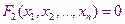
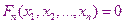
Наряду с системой, решение которой необходимо найти, мы решаем систему из такого же числа уравнений решение которой известно.

……………………

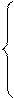
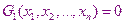
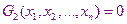
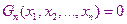
Деформируя (возмущая) уравнение системы с известным решением, с помощью конечного числа N (малых приращений), преобразуем их к системе, решение которой надо найти.

Деформацию можно проводить различными способами.

Например, на шаге деформации с номером k деформацию можно записать в виде

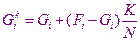, где i – это номер уровня.

Если число шагов деформации N достаточно велико, то деформация системы на каждом шаге будет не значительна.

Решение системы (G) можно использовать как начальное приближение неизвестных для итерационного решения полученного при первой деформации системы. Так как эта система при достаточно больших значениях N мало отличается от предыдущей то, вероятно, что сходимость для деформируемой системы будет обеспечена.

После этого производится вторая деформация. И используя решения, полученные для первой деформации в качестве начального приближения, найдём корень системы после второй деформации. В конце счета, когда номер деформации k= N решаемая система становится эквивалентной исходной (F).