Численное интегрирование

Из курса математического анализа известно, что, если функция f(x) непрерывна на отрезке [a;b] и дифференцируема, то определенный интеграл от этой функции в пределах от a до b существует и может быть вычислен по формуле Ньютона-Лейбница:

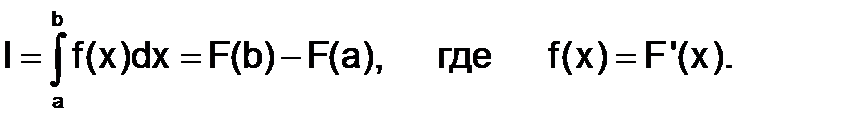
Если первообразную функцию F(x) не удается выразить аналитически через элементарные функции или если при проведении практических расчетов подынтегральная функция f(x) задается в виде таблицы, то это приводит к необходимости замены аналитического интегрирования численными методами.

Для функции f(x), заданной в прямоугольной системе координат на интервале [a;b], этот интеграл численно равен площади, ограниченной кривой f(x), осью Ox и двумя ординатами ac и bd.

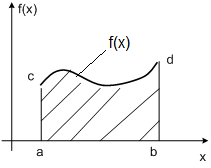
Рис. 1.4.1-1

Задача численного интегрирования заключается в нахождении значения определенного интеграла через ряд значений подынтегральной функции y_i=f(x_i), заданной в точках x_i (i=0,1,…,n). Причем, x₀ = a, x_n= b. Чаще всего интервал разбивают на подынтервалы длинойh = x_i+1 - x_i.

Применительно к однократному интегралу, формулы численного интегрирования представляют собой квадратурные формулы вида:

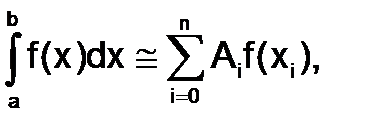
гдеA_i – числовые коэффициенты, называемые весами квадратурной формулы, аx_i – точки из отрезка - узлами квадратурной формулы, n> 0 – целое число.

Искомый определенный интеграл можно представить в виде суммы интегралов:

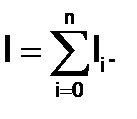
На каждом i-м отрезке функция аппроксимируется(заменяется) некоторой другой легко интегрируемой функцией g_i(x). В результате получаем следующую квадратурную формулу:

.

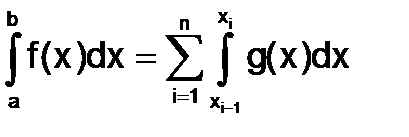Для решения поставленной задачи подынтегральнуюфункцию f(x)необходимо заменить приближенной функцией, которая может быть проинтегрирована в аналитическим виде. В качестве такой функции обычно используют полином Р(х)с узлами интерполяции в точках х₀, х₁, х₂, …,х_n. В этих точках значения функции и интерполяционного полинома полностью совпадают f(x_i) = Р(x_i).

Для получения простых формул интегрирования используют полиномы нулевой, первой и второй степени и соответственно получают формулы численного интегрирования: прямоугольников, трапецийиСимпсона.

Очевидно, что замена функции f(x) интерполирующим полиномом приводит к образованию погрешности вычисления значения интеграла

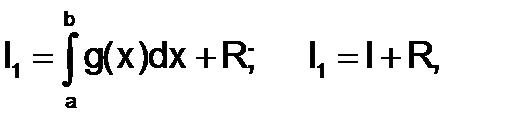
где I₁ – точное значение интеграла, I – значение интеграла, вычисленного численным методом, а 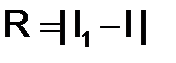– погрешность метода.

Отметим, что увеличение числа подынтервалов n (или уменьшение длины шага интегрирования h) ведет к уменьшению погрешности.