Уточнение решения (итерационный метод).

Решения, получаемые с помощью прямых методов обычно содержат погрешности. В ряде случаев, особенно если объём системы велик, эти погрешности могут быть значительными.

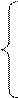Рассмотрим итерационный процесс позволяющий уточнить решения на следующем итерационном шаге. Пусть решается система

……………………………

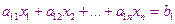
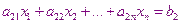
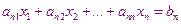
Пусть на k-ом итерационном шаге получено решение в виде 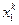, ,…, , 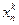где k-это номер итерационного шага.

Подставим полученное решение в левые части уравнений системы, результат вычислений этих уравнений обозначим , , .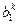

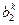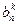В результате получим систему

……………………………

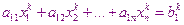
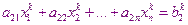
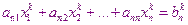
Вычтем из каждого уравнения 1-ой системы уравнение 2-ой системы и получим систему вида

……………………………

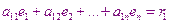
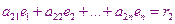
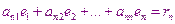
Отсюда

Это невязка для уравнений с соответствующим номером.

Теперь мы получаем систему решением, которой будут соотношения уточняющие решение.

………………..

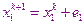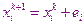
Преимуществом этого метода является то, что на каждом итерационном шаге решается система с одной и той же матрицей. Это позволяет оптимизировать вычислительный процесс, строить экономичные алгоритмы.

Метод 17