Решение обыкновенных дифференциальных уравнений (ОДУ).
К решению дифференциальных уравнений приводит большое число научно-исследовательских задач и задач инженерной практики, но лишь не многие из них удается решить аналитически, поэтому численные методы решения дифференциальных уравнений играют такую важную роль в инженерной практике.
Дифференциальные уравнения, содержащие одну независимую переменную и производные по ней, называются обыкновенными дифференциальными уравнениями.
Для решения дифференциального уравнения необходимо задание дополнительных условий, если дополнительные условия задаются при одном значении независимой переменной, то такие условия называются начальными, а задача решения уравнения называется задачей с начальными условиями или задача Коши.
Если условия задаются при двух или более значениях переменной, то такие условия называются граничными, а задачу называют краевой.
В задаче Коши роль независимой переменной играет величина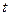 
(время), а дополнительное условие для начального момента времени ( 
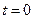). В краевых задачах в качестве независимой переменной выступает координата отрезка, а граничные условия задаются в начале и конце отрезка.
Для решения задачи Коши и краевой принимают различные численные методы. Часто краевую задачу решают путем сведения её к задаче Коши. Отсюда следует, что обычно задачи Коши являются более легкими для численного решения.
При численном решении вводится шаг по координате, и решение находится в точках отстоящих друг от друга на величину шага. Для решения задачи Коши разработано множество методов, которые можно разделить на 2 группы:
1 группа – одношаговые методы.
В них для нахождения решения в следующей точке (удаленной на расстояние h) требуется информация лишь об одном предыдущем шаге.
2 группа – многошаговые методы.
Методы прогноза и коррекции.
В них для нахождения значения в следующей точке требуется информация из нескольких предыдущих точек.
При численном решении дифференциальных уравнений можно выделить 3 типа погрешности:
1)погрешность округления;
2)погрешность усечения, связана с аппроксимацией бесконечных рядов несколькими первыми членами, обусловлена численным методом;
3)погрешность распространения, она является результатом накопления погрешностей появившихся на предыдущих этапах счета.
Метод 28
Метод Эйлера.
Простейшим методом решения обыкновенного дифференциального уравнения первого порядка является метод Эйлера.
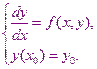
Требуется найти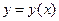 
. Как 
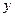зависит от 
.
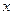Будем находить решение в точках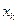 
отстоящих друг от друга на расстоянии h (шаг задачи). Допустим решение в точке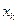 
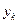известно, и требуется найти значение неизвестной 
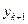в точке 
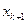. Разложим решение в окрестности точки 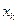в ряд Тейлора:
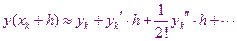
В этом ряде ограничимся первыми двумя слагаемыми
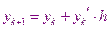
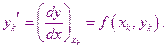
В результате получаем простейшую формулу
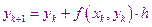, которая реализует метод Эйлера .
, 
,
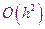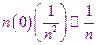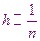
точность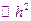 
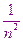погрешность на одном шаге.
Таким образом, погрешность метода Эйлера равна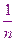 
.
Метод 29
Дата добавления: 2017-03-12; просмотров: 1539;
Поиск по сайту
Узнать еще
- I. Решение логических задач средствами алгебры логики
- II. Решение логических задач табличным способом
- III. Решение логических задач с помощью рассуждений
- АВТОЗВУК РЕШЕНИЕ ПРОБЛЕМ
- Автомодельного ламинарного течения жидкости в трубе с использованием системы дифференциальных уравнений, описывающих течение жидкости в трубе
- Акустическое разрешение диатонических интервалов
- АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- Алгоритмы нахождения корней уравнений.
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
