Значення частинних коефіцієнтів регресії

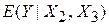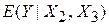Значення частинних коефіцієнтів полягає в такому: є мірою зміни середньої величини Y, при одиничній зміні Х₂ за умови того, що Х₃ не змінюється. Іншими словами, дає степінь нахилу по відношенню до Х₂, коли Х₃ не змінюється. Зазначимо також, що 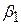і є частинними похідними 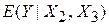по Х₂ і Х₃ відповідно. Аналогічно 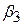є мірою зміни середньої величини У при одиничній зміні Х₃, коли Х₂ не змінюється. Тобто він дає «прямий», або «нетто», ефект одиничної зміни Х₃ на середню величину Y за вирахуванням впливу Х₂.

Яке точне значення терміна «залишаючи постійною»? Щоб зрозуміти це, припустимо, що Y характеризує випуск продукції, а Х₂ і Х₃ – трудовитрати й капітал відповідно. Припустимо далі, що для виробництва Y потрібні і Х₂, і Х₃, і що пропорція, у якій вони можуть бути використані у виробництві Y, може варіюватися. Тепер припустимо, що ми збільшили на одиницю трудовитрати, очевидно, це приведе до деякого збільшення випуску продукції. Ми не можемо пояснювати результуючу зміну випуску продукції виключно збільшенням витрат Х₂, бо в такому разі збільшиться внесок Х₂ в Y, оскільки Х₂ одержує кредит за частину зміни в Y внаслідок збільшення капіталу. Отже, щоб оцінити «істинний внесок» Х₂ в зміну Y, ми повинні контролювати вплив від Х₂.

Процедура подібного контролю така. Припустимо, що ми хочемо контролювати лінійний вплив капіталу Х₃ на випуск продукції, при зміні трудовитрат Х₂ на одиницю. Здійснюємо це в три етапи.

1. Регресуємо Y тільки за Х₃ таким чином:

.

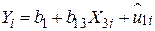(5.3.1)

Рівняння (5.3.1) являє собою рівняння двовимірної регресії. При цьому індекс 1 стосується змінної Y, а 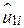позначає залишкову складову за наслідками вибірки.

2. Регресуємо Х₂ тільки за змінною Х₃:

,

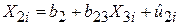(5.3.2)

де 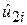– залишкова складова. Маємо

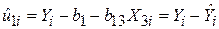;	(5.3.3)
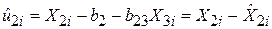,	(5.3.4)

де 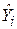і 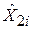– оцінені величини з регресійних моделей (5.3.1) і (5.3.2) відповідно.

Яке значення залишків 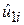і 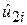? Складова 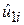позначає величину 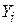після вилучення лінійного впливу на неї Х₃. Аналогічно 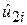позначає величину 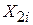після вилучення впливу на неї Х₃. Отже, 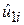і 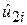– «звільнені від впливу Х₃ величини» 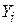і .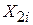

3. Отже, якщо ми проведемо регресійний аналіз 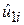і 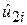у вигляді

,

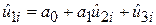(5.3.5)

де 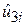– залишкова складова по вибірці, то а₁ повинен дати оцінку «істинного, або звільненого, ефекту» від одиничної зміни Х₂ на Y або істинний нахил Y по відношенню до Х₂, тобто оцінку .

За МНК а₁ можна подати у вигляді

.

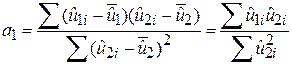Оскільки 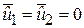, то рівняння (5.3.1) і (5.3.2) можна переписати у вигляді

; ,

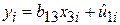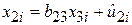де малі букви використовуються для позначення величин у формі відхилень. Отримаємо з цих рівнянь 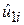і :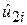

;

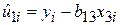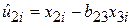
і підставимо їх у вирази для а₁:

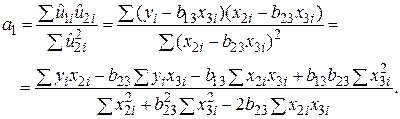
Враховуючи, що

, ,

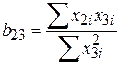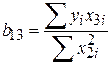одержуємо

.

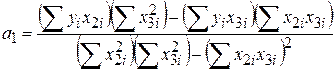Як буде показано в наступному параграфі, цей вираз збігається з оцінкою за МНК. Таким чином, на практиці немає необхідності здійснювати всі розрахунки, оскільки а₁ обчислюється за достатньо простими формулами.