Модель із трьома змінними. Позначення і гіпотези
Узагальнюючи функцію PRF з двома змінними, ми можемо записати її для трьох змінних таким чином:
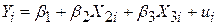 , ,
| (5.1.1) |
де Y – залежна змінна; Х2 і Х3 – пояснювальні змінні, або регресори; u – стохастичний збурююча складова; i – спостереження; для випадку тимчасових рядів замість індексу i використовуєтьсяіндекс t.
У (5.1.1) 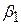 – складова, що визначає точку перетину. Як завжди, він має середню дію на Y всіх змінних, виключених із моделі, хоча його механічна інтерпретація є середня величина Y при Х2 і Х3, що дорівнюють нулю. Коефіцієнти
– складова, що визначає точку перетину. Як завжди, він має середню дію на Y всіх змінних, виключених із моделі, хоча його механічна інтерпретація є середня величина Y при Х2 і Х3, що дорівнюють нулю. Коефіцієнти 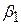 і
і  зазвичай називають частинними регресійними коефіцієнтами.
зазвичай називають частинними регресійними коефіцієнтами.
Ми продовжуватимемо оперувати в рамках схеми класичної лінійної регресійної моделі (CLRM). Зокрема, ми припускаємо, що:
- середня величина 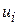 дорівнює нулю:
дорівнює нулю:
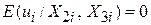 для всіх i; для всіх i;
| (5.1.2) |
- серійна кореляція відсутня:
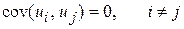 ; ;
| (5.1.3) |
- має місце гомоскадастичність:
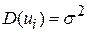 ; ;
| (5.1.4) |
- коваріація 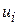 і кожної змінної Х дорівнюють нулю:
і кожної змінної Х дорівнюють нулю:
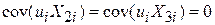 ; ;
| (5.1.5) |
- модель коректно специфікована; (5.1.6)
- відсутня точна колінеарність між змінними Х, тобто
відсутній точний лінійний зв’язок між Х2 і Х3. (5.1.7)
Крім того, ми припускаємо, що множинна регресійна модель лінійна за параметрами, величини регресорів фіксовані в повторних вибірках і регресори змінюються достатньою мірою.
Логічна обґрунтованість гіпотез (5.1.2) – (5.1.6) та ж, що була наведена в розд. 3.2. Гіпотеза (5.1.7) про відсутність точного лінійного зв’язку між Х2 і Х3, відома як гіпотеза про відсутність колінеарності або мультиколінеарності, якщо є можливість існування більше ніж одного лінійного співвідношення, є новою і потребує деякого пояснення.
Відсутність колінеарності означає, що ніяка з пояснювальних змінних не може бути зображена у вигляді лінійної комбінації решти змінних. Це можна пояснити на прикладі діаграми (рис.5.1).
а б
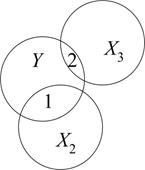
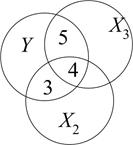
Рис. 5.1. Діаграма, що демонструє відсутність (а) і наявність колінеарності (б)
На рис.5.1 коло Y зображає варіацію залежної змінної Y, а кола Х2 і Х3 зображають, відповідно, варіації регресорів Х2 і Х3. На рис.5.1, а область 1 зображає варіацію в Y, пояснену за рахунок Х2, а область 2 – варіацію в Y, пояснену за рахунок Х3. Області 3 і 4 (рис.5.1, б) зображають варіацію в Y, пояснену через Х2, а області 4 і 5 – пояснену через Х3. Але, оскільки область 4 є загальною для Х2 і Х3, ми не можемо назвати а priori, яка частина 4 належить Х2, а яка – Х3. Загальна область 4 представляє випадок колінеарності. Гіпотеза відсутності колінеарності вимагає відсутності перекриття між Х2 і Х3, тобто загальна область 4 повинна бути нульовою. Іншими словами, ми хочемо мати справу із ситуацією, зображеною на рис.5.1, а.
Формально відсутність колінеарності означає, що немає таких чисел 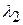 і
і 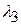 , які одночасно не є нулями, що
, які одночасно не є нулями, що
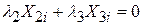 . .
| (5.1.8) |
Якщо ж подібне лінійне співвідношення виконується, тоді говорять, що Х2 і Х3 колінеарні або лінійно залежні. Якщо ж (5.1.8) виконується тільки при 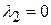 і
і 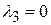 , то говорять, що Х2 і Х3 лінійно незалежні.
, то говорять, що Х2 і Х3 лінійно незалежні.
Так, якщо
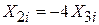 або або 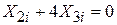 , ,
| (5.1.9) |
то дві змінні лінійно залежні, і якщо обидві вони включені в регресійну модель, ми матимемо точну колінеарність або точну лінійну залежність між двома змінними.
Припустимо тепер, що 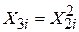 . Чи буде при цьому порушена гіпотеза відсутності колінеарності? Ні, оскільки зв’язок між регресорами нелінійний і не порушується вимога про відсутність лінійного зв’язку між регресорами.
. Чи буде при цьому порушена гіпотеза відсутності колінеарності? Ні, оскільки зв’язок між регресорами нелінійний і не порушується вимога про відсутність лінійного зв’язку між регресорами.
Пояснимо обґрунтованість гіпотези відсутності колінеарності на прикладі. Припустимо, що в (5.1.1) Y, Х2 і Х3 представляють витрати на споживацькі товари, дохід і заощадження покупця відповідно. Постулюючи лінійний зв’язок між споживацькими витратами, доходом і заощадженнями, економічна теорія припускає, що дохід і заощадження мають деякий незалежний вплив на витрати. Якщо це не так, то не має сенсу включати їх у модель по окремості. На противагу цьому, якщо існує точна лінійна залежність між доходом і накопиченням, то ми маємо всього одну незалежну змінну, а не дві, і немає способу оцінити роздільний вплив на витрати доходу і заощаджень. Для більшої виразності покладемо 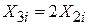 в регресійній моделі «витрати-прибуток-заощадження». Тоді (5.1.1) можна подати у вигляді
в регресійній моделі «витрати-прибуток-заощадження». Тоді (5.1.1) можна подати у вигляді
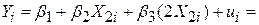
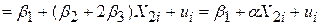 , ,
| (5.1.10) |
де 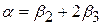 . Тобто ми фактично маємо регресійну модель із двома змінними, а не з трьома. Крім того, якщо ми застосовуємо (5.1.10) і отримаємо a, то не зможемо оцінити роздільний вплив Х2 (=b2) і Х3 (=b3) на Y.
. Тобто ми фактично маємо регресійну модель із двома змінними, а не з трьома. Крім того, якщо ми застосовуємо (5.1.10) і отримаємо a, то не зможемо оцінити роздільний вплив Х2 (=b2) і Х3 (=b3) на Y.
Підводячи підсумки зазначимо, що гіпотеза про відсутність мультиколінеарності вимагає, щоб у функцію PRF включали тільки ті змінні, які не є лінійними функціями деяких інших змінних моделі.
Дата добавления: 2016-07-27; просмотров: 1782;











