Інтерпретація простого і частинного коефіцієнтів кореляції
У разі моделі з двома змінними R мав чітке визначення, він визначав степінь лінійної зв’язаності між залежною змінною Y і єдиною пояснювальною змінною Х. Якщо ж ми виходимо за рамки моделі з двома змінними, нам потрібно приділити увагу простому коефіцієнту кореляції. З рівності (5.8.2), наприклад, бачимо, що:
1. Якщо навіть 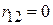 , то
, то 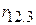 не буде нульовим за умови, що не дорівнюють нулю
не буде нульовим за умови, що не дорівнюють нулю  і
і 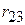 (або обидва вони дорівнюють нулю).
(або обидва вони дорівнюють нулю).
2. Якщо 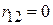 , а
, а  і
і 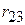 ненульові і мають однакові знаки, то
ненульові і мають однакові знаки, то 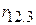 буде негативним, якщо ж вони мають протилежні знаки, він буде позитивним. Приклад допоможе краще зрозуміти це. Нехай Y позначає урожай сільгоспкультури, X2 - опади, а X3 – температуру. Припустимо, що
буде негативним, якщо ж вони мають протилежні знаки, він буде позитивним. Приклад допоможе краще зрозуміти це. Нехай Y позначає урожай сільгоспкультури, X2 - опади, а X3 – температуру. Припустимо, що 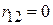 , тобто немає зв’язку між урожаєм і опадами. Припустимо далі, що
, тобто немає зв’язку між урожаєм і опадами. Припустимо далі, що 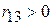 і
і 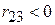 . Тоді, як бачимо з (5.8.2),
. Тоді, як бачимо з (5.8.2),  . Тобто при незмінній температурі існує позитивний зв’язок між урожаєм і опадами. Цей, здавалося б, парадоксальний результат, відповідає дійсності, оскільки температура X3 впливає і на урожай Y і на опади X2. Для знаходження істинного співвідношення між урожаєм і опадами необхідно виключити вплив температури. На цьому прикладі показано, як можна помилятися, використовуючи простий коефіцієнт кореляції.
. Тобто при незмінній температурі існує позитивний зв’язок між урожаєм і опадами. Цей, здавалося б, парадоксальний результат, відповідає дійсності, оскільки температура X3 впливає і на урожай Y і на опади X2. Для знаходження істинного співвідношення між урожаєм і опадами необхідно виключити вплив температури. На цьому прикладі показано, як можна помилятися, використовуючи простий коефіцієнт кореляції.
3. Значення 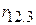 і
і 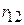 не обов’язково повинні мати однакові знаки. Це зауваження стосується й інших коефіцієнтів кореляції.
не обов’язково повинні мати однакові знаки. Це зауваження стосується й інших коефіцієнтів кореляції.
4. Для двовимірної регресії, як нам відомо, величина R2 лежить між 0 і 1. Ця властивість залишається справедливою і для квадратів частинних коефіцієнтів кореляції. Спираючись на цей факт, можна перевірити справедливість властивості
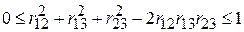 . .
| (5.8.5) |
5. Припустимо, що  . Чи означає це, що й
. Чи означає це, що й 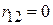 ? Відповідь очевидна з (5.8.5). Некорельованість Y і X3, а також X2 і X3, не спричиняє корельованості Y і X2.
? Відповідь очевидна з (5.8.5). Некорельованість Y і X3, а також X2 і X3, не спричиняє корельованості Y і X2.
Побіжно відзначимо, що вираз 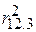 можна назвати коефіцієнтом частинної детермінації й інтерпретувати його як частину варіації Y, пояснену не за рахунок змінної X3, а через включену в модель змінну X2. Таке трактування
можна назвати коефіцієнтом частинної детермінації й інтерпретувати його як частину варіації Y, пояснену не за рахунок змінної X3, а через включену в модель змінну X2. Таке трактування 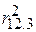 стає зрозумілим, якщо застосувати формулу
стає зрозумілим, якщо застосувати формулу
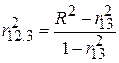 . .
|
Відзначимо також співвідношення між  , простими коефіцієнтами кореляції та частинними кореляційними коефіцієнтами:
, простими коефіцієнтами кореляції та частинними кореляційними коефіцієнтами:
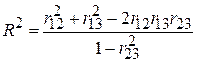 ; ;
| (5.8.6) |
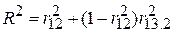 ; ;
| (5.8.7) |
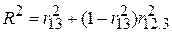 . .
| (5.8.8) |
Відзначимо на закінчення таке. Раніше мова йшла про те, що  не спадає при включенні в модель додаткових пояснювальних змінних. Це зрозуміло з рівності (5.8.7), яка також показує, що частина варіації Y, поясненої спільно змінними X2 і X3, має 2 складники: частина, пояснена тільки X2 (це
не спадає при включенні в модель додаткових пояснювальних змінних. Це зрозуміло з рівності (5.8.7), яка також показує, що частина варіації Y, поясненої спільно змінними X2 і X3, має 2 складники: частина, пояснена тільки X2 (це 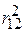 ), і частина, непояснена X2 (це
), і частина, непояснена X2 (це 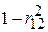 ), помножена на пояснену змінною X3 частину при постійному значенні X2. Оскільки
), помножена на пояснену змінною X3 частину при постійному значенні X2. Оскільки  , то
, то 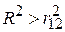 . У крайньому випадку при
. У крайньому випадку при 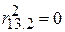 маємо
маємо 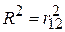 .
.
Дата добавления: 2016-07-27; просмотров: 2546;











