Оцінка частинних коефіцієнтів регресії за МНК
Для знаходження за МНК оцінок для параметрів запишемо SRF, що відповідає PRF з (5.1.1), у вигляді
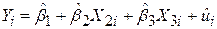 , ,
| (5.4.1) |
де 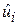 – залишкова складова, відповідна стохастичній збурюючій складовій в
– залишкова складова, відповідна стохастичній збурюючій складовій в 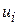 .
.
Як було відзначено раніше, процедура МНК полягає у виборі величин невідомих параметрів таким чином, щоб сума квадратів залишків (RSS) 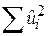 була якомога меншою. Із (5.4.1) одержуємо
була якомога меншою. Із (5.4.1) одержуємо
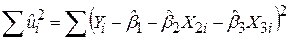 . .
| (5.4.2) |
Відповідно до процедури МНК знаходимо частинні похідні:
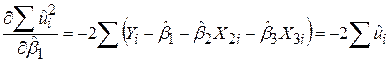 ; ;
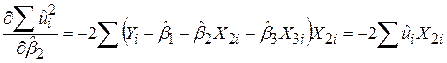 ; ;
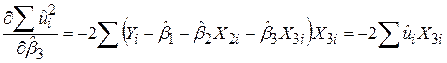 . .
|
Прирівнюючи до нуля ці вирази, одержуємо систему алгебраїчних рівнянь щодо коефіцієнтів регресії:
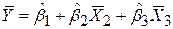 ; ;
| (5.4.3) |
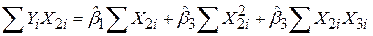 ; ;
| (5.4.4) |
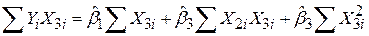 . .
| (5.4.5) |
Із рівняння (5.4.3) одержуємо величину для 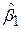 :
:
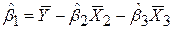 . .
| (5.4.6) |
Для 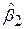 і
і 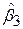 можна отримати, розв’язуючи (5.4.3)–(5.4.5), такі вирази:
можна отримати, розв’язуючи (5.4.3)–(5.4.5), такі вирази:
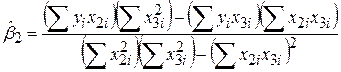 ; ;
| (5.4.7) |
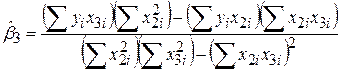 . .
| (5.4.8) |
При цьому малі букви використовуються для позначення значень змінних у відхиленнях.
Примітки:
1. Рівняння (5.4.7) і (5.4.8) симетричні в тому значенні, що одне може бути отримане з іншого заміною Х2 на Х3 і навпаки.
2. Знаменники в обох формулах однакові.
3. Тривимірний випадок є природним узагальненням двовимірної моделі.
На закінчення розглянемо випадок, коли модель містить k параметрів регресії:
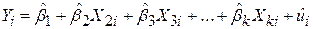 . .
|
Відповідно до МНК нам необхідно мінімізувати суму квадратів відхилень
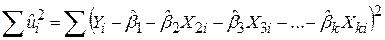 . .
|
За вже відомою нам процедурою одержуємо
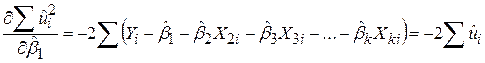 ; ;
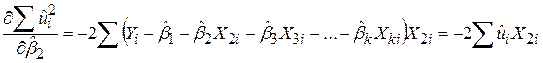 ; ;
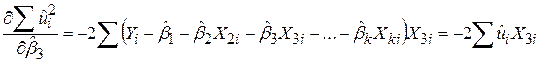 ;
.............................. ;
..............................
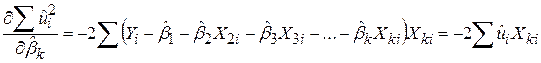 . .
|
Отримуємо таку систему лінійних алгебраїчних рівнянь:
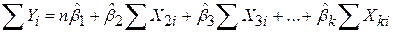 ; ;
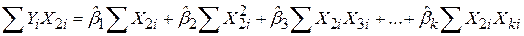 ; ;
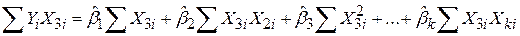 ;
........................... ;
...........................
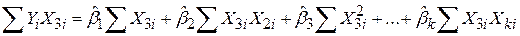 . .
|
Переходячи до малих букв, цю систему можна переписати в такому вигляді:
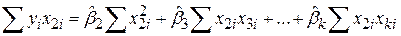 ; ;
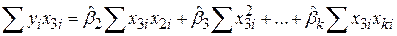 ;
........................... ;
...........................
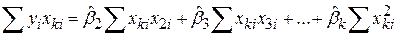 . .
|
Відзначимо також, що регресійна модель з k змінними задовольняє таким рівнянням:
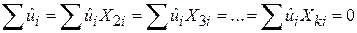 . .
|
Дата добавления: 2016-07-27; просмотров: 1755;











