Ілюстративний приклад у матричних позначеннях
Підводячи підсумки використання матричного апарату, розглянемо числовий приклад для моделі з трьома змінними. Пригадаємо приклад для регресії сукупних особистих витрат на споживання за сукупним особистим доходом і часом на період 1956–1970 рр. Наголошувалося, що змінна тренда t може зображувати серед іншого сукупне населення: сукупні витрати на споживання повинні збільшуватися зі зростанням населення. Одним зі шляхів для ізолювання впливу зростання населення є перехід до сукупних витрат і сукупного доходу на душу населення. Регресія сукупних витрат на душу населення залежно від сукупного доходу на душу населення дасть співвідношення між витратами і доходом незалежно від зміни населення. Змінна тренда може залишатися в моделі для обліку впливу на витрати інших чинників (наприклад, технології). Отже, модель регресії може бути зображена у вигляді
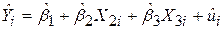 , ,
| (9.10.1) |
де Y – витрати на душу населення; X2 – дохід на душу населення; X3 – час. У табл. 9.4 подані необхідні для цієї моделі дані.
Таблиця 9.4
Витрати на споживання на душу населення (PPCE) і
дохід на душу населення (PPDI) в США за 1956–1970 рр.
| PPCE, Y | PPDI, X2 | Час, X3 |
| 1 (1956) | ||
| 15 (1970) |
У матричних позначеннях наша задача може бути зображена в такому вигляді:
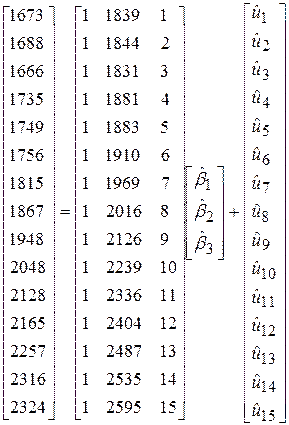
| (9.10.2) |
За наведеними даними можна отримати значення величин:
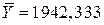 , , 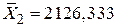 , , 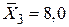 , , 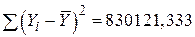 ; ;
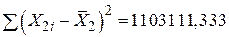 , , 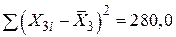 ; ;
| ||
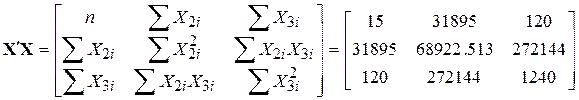 ; ;
| ||
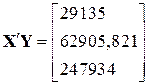 , , 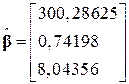 . .
| (9.10.3) | |
Сума квадратів залишків може бути підрахована за формулою
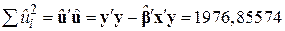 . .
| (9.10.4 |
Звідси можна отримати
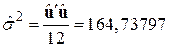 . .
| (9.10.5) |
Матрицю варіацій можна обчислити за такою формулою
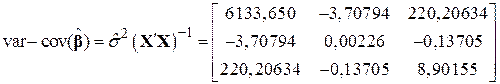 . .
| (9.10.6) |
Діагональні елементи цієї матриці дають значення дисперсій коефіцієнтів 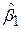 ,
, 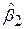 і
і 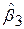 , а корінь квадратний із них дає значення стандартної похибки.
, а корінь квадратний із них дає значення стандартної похибки.
За наведеними даними можна легко перевірити, що
| ESS=828144,47786; | (9.10.7) |
| TSS=830121,333. | (9.10.8) |
Отже,
| R2=0,99761. | (9.10.9) |
Застосовуючи формулу (7.8.4) можна визначити наведений коефіцієнт детермінації
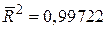 . .
| (9.10.10) |
Підсумовуючи отримані результати, одержуємо
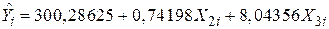 ,
(78,31763) (0,04753) (2,98354)
t = (3,83421) (15,61077) (2,69598)
R2=0,99761, ,
(78,31763) (0,04753) (2,98354)
t = (3,83421) (15,61077) (2,69598)
R2=0,99761, 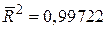 , DF=12. , DF=12.
| (9.10.11) |
Інтерпретація результатів (9.10.14). Якщо обидві величини Х2 і Х3 набувають фіксованих нульових значень, то середня величина витрат на душу населення складає приблизно 300 дол. 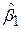 повинна братися з великою обережністю. Частинний коефіцієнт регресії
повинна братися з великою обережністю. Частинний коефіцієнт регресії 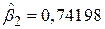 означає, що не змінюючи інші змінні, зростання доходів приводить до збільшення витрат на споживання на душу населення на 0,74 дол. Коротше кажучи, оцінка граничної схильності до споживання складає приблизно 74%. Аналогічно, не змінюючи інших змінних, середні витрати на споживання зростають за рік приблизно на 8 дол. за досліджуваний період. Величина R2=0,99761 показує, що взяті дві пояснювальні змінні дозволяють врахувати більше 99% дисперсії витрат на споживання на душу населення в США за даний період. Хоча
означає, що не змінюючи інші змінні, зростання доходів приводить до збільшення витрат на споживання на душу населення на 0,74 дол. Коротше кажучи, оцінка граничної схильності до споживання складає приблизно 74%. Аналогічно, не змінюючи інших змінних, середні витрати на споживання зростають за рік приблизно на 8 дол. за досліджуваний період. Величина R2=0,99761 показує, що взяті дві пояснювальні змінні дозволяють врахувати більше 99% дисперсії витрат на споживання на душу населення в США за даний період. Хоча 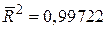 трохи менше, ніж R2, проте цей коефіцієнт залишається дуже високим.
трохи менше, ніж R2, проте цей коефіцієнт залишається дуже високим.
Переходячи до аналізу статистичної значущості коефіцієнтів регресії, ми відзначаємо з (9.10.14), що кожний окремий коефіцієнт регресії статистично значимий, скажімо, при 5%-му рівні значущості (з таблиць ми бачимо, що критичне значення t для DF=12є 2.179). Кожна з підрахованих t-величин більша, ніж цезначення. Отже, ми можемо відхиляти нульові гіпотези про нульові значення величин істинних коефіцієнтів регресії.
Як уже було відзначено раніше, ми не можемо застосувати результати t-тестудля перевірки гіпотези про те, що 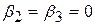 , оскільки процедура t-тесту припускає, що при проведенні тесту кожного разу проводиться незалежна вибірка. Якщо ж одна й та сама вибірка використовується для перевірки гіпотез одночасно для
, оскільки процедура t-тесту припускає, що при проведенні тесту кожного разу проводиться незалежна вибірка. Якщо ж одна й та сама вибірка використовується для перевірки гіпотез одночасно для  і
і 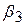 , то ймовірно, що оцінки
, то ймовірно, що оцінки 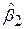 і
і 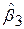 від’ємно корельовані (коваріація між ними складає –0,13705). Тому ми не можемо застосовувати t-тестдля перевірки гіпотези про те, що
від’ємно корельовані (коваріація між ними складає –0,13705). Тому ми не можемо застосовувати t-тестдля перевірки гіпотези про те, що 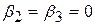 .
.
Для перевірки цієї гіпотези може бути застосований і F-тест, розглянутий нами в розд. 8. Для використовування F-тестунам необхідні дані ANOVA-таблиці.
Таблиця 9.5
ANOVA-таблиця для даних з таблиці 9.4.
| Джерело дисперсії | SS | DF | MSS |
| Унаслідок Х2 і Х3 | 828144,47786 | 414072,3893 | |
| Унаслідок залишків | 1976,85574 | 164,73797 | |
| Загальна | 830121,33360 |
За результатами цієї таблиці звичайним способом одержуємо
| F=2513,52. | (9.10.12) |
Підрахована величина значно перевершує критичне значення F-розподілуз 2 і 12 степенями вільності. Отже, ми можемо відкинути гіпотезу про те, що 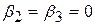 , тобто, що витрати на споживання на душу населення не пов’язані лінійно з доходом і трендом.
, тобто, що витрати на споживання на душу населення не пов’язані лінійно з доходом і трендом.
Раніше ми розглядали застосування регресійної моделі для побудови як середнього, так й індивідуального прогнозів. Припустимо, що для 1971 р. дохід на душу населення складав 2 610 дол., і ми хочемо спрогнозувати відповідні йому витрати на споживання. У такому разі середній і індивідуальний прогнози витрат на душу населення
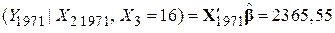 . .
| (9.10.13) |
Як відомо, дисперсія величин 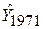 і
і 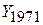 визначається за формулами
визначається за формулами
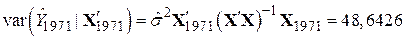 ; ;
| (9.10.14) |
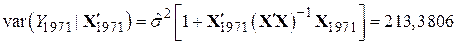 . .
| (9.10.15) |
Стандартні похибки наведених величин мають такі значення:
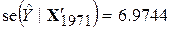 , , 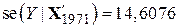
| (9.10.16) |
Довірчі інтервали для прогнозованих величин при 5%-му рівні значущості визначаються за формулами
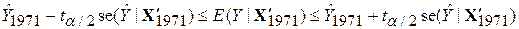 ; ;
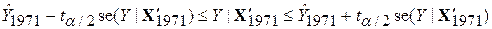 . .
| (9.10.17) |
Підставляючи в (9.10.20) значення вхідних величин, одержуємо такі довірчі інтервали:
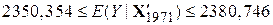 ; ;
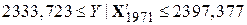 . .
| (9.10.18) |
Раніше нами було введене поняття кореляційної матриці R. Для нашого випадку кореляційна матриця має вигляд
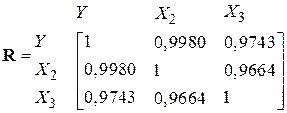 . .
| (9.10.19) |
Висновок
Основною метою розділу є ознайомлення з матричним підходом до класичної лінійної моделі регресії. Хоча була введена досить незначна кількість нових понять, проте матричні позначення дають компактний метод опису лінійної моделі регресії, що містить довільну кількість змінних.
[1] Galton F. Family Likeness in Stature // Proceedings Royal Society. - L., 1886. - Vol.40. - p.42-72.
Дата добавления: 2016-07-27; просмотров: 1775;











