Властивості оцінювачів за МНК

Властивості оцінювачів за МНК для множинної регресійної моделі аналогічні властивостям для двовимірного випадку. А саме:

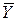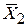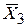1. Тривимірна поверхня (площина) регресії проходить через середні , і . Це очевидно з (5.4.3). Ця властивість допускає узагальнення на випадок лінійної регресійної моделі з k змінними (один регресант і (k–1) регресорів):

.

(5.4.20)

Для цієї моделі виконується

.

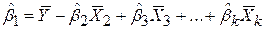(5.4.21)

2. Середня величина оцінки 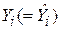дорівнює середній величині дійсних 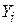, що легко доводиться:

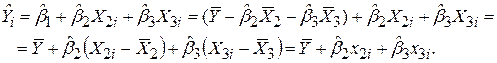
(5.4.22)

Підсумовуючи обидві частини (5.4.22) за об’ємом усієї вибірки і поділяючи на N, одержуємо 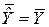. При цьому використовується відома властивість 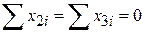. Зауважимо також, що з (5.4.22) випливає рівність

,

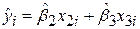(5.4.23)

де .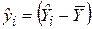

Отже, SRF (5.4.1) може бути поданий у формі відхилень

.

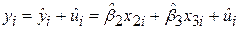(5.4.24)

3. 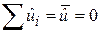. Ця рівність є наслідком МНК.

4. Залишки 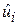некорельовані з 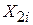і 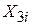, тобто .

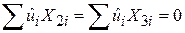5. Залишки 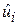некорельовані з 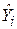, тобто 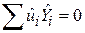. Цю властивість легко довести, якщо обидві частини рівності 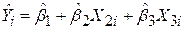помножити на 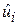і підсумувати за об’ємом вибірки з урахуванням властивості 4.

6. Із (5.4.12) і (5.4.15) бачимо, що зі зростанням до 1 кореляційного коефіцієнта R²₃ між Х₂ і Х₃ дисперсі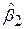ї і 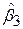при фіксованих значеннях s² і 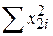, також зростають. Коли R²₃=1 (точна колінеарність), ці дисперсії стають необмеженими. Тобто зі зростанням R²₃ значення і 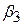стають усе більш невизначеними.

7. Із (5.4.12) і (5.4.15) зрозуміло, що для даних величин R²₃, 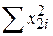, дисперсії коефіцієнтів 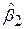і 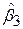прямо пропорційні s², тобто зі зростанням s² вони зростають. Водночас для даних величин s₂ і R²₃ дисперсія 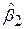обернено пропорційна 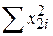, тобто чим більше змінюється за вибіркою Х₂, тим менша дисперсія 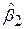і, отже, тим точніше можна оцінити . Аналогічний висновок можна зробити про дисперсію .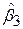

8. При прийнятих гіпотезах класичної лінійної регресійної моделі можна показати, що оцінки за МНК частинних коефіцієнтів регресії не тільки лінійні й незміщені, але й мають якнайменшу дисперсію в класі лінійних незміщених оцінок, тобто вони мають властивість BLUE.

5.5. Коефіцієнт детермінації R²і коефіцієнт кореляції множинної регресійної моделі

У випадку моделі з двома змінними ми бачимо, що коефіцієнт

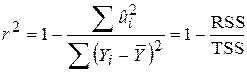
виміряв якість підгонки рівняння регресії, точніше, він дав співвідношення або відсоток у загальній варіації Y, пояснений за рахунок пояснювальної змінної Х. Даний підхід може бути узагальненим на випадок моделей, які містять більше двох змінних. Так, у моделі з трьома змінними нас цікавить, яка частина у варіації У пояснюється за рахунок змінних Х₂ і Х₃. У цьому випадку коефіцієнт позначається R² і називається коефіцієнтом детермінації множинної регресії. Концептуально він наближений до R².

Для виведення R² можна скористатися процедурою виведення R², описаною в підрозд. 2.5. Пригадаємо, що

.

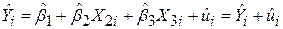(5.5.1)

Переходячи до малих букв, цю рівність можна записати у вигляді

.

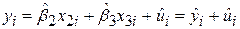(5.5.2)

Підносячи (5.5.2) до квадрата й підсумовуючи, одержуємо

.

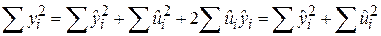(5.5.3)

Ця рівність показує, що загальна сума квадратів (TSS) дорівнює поясненій сумі квадратів (ESS) + сума квадратів залишків (RSS). Підставляючи замість 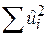вираз (5.4.19), одержуємо

.

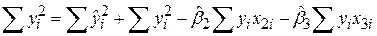Звідси одержуємо вираз для ESS пояснюючої суми квадратів:

.

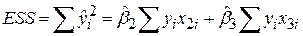(5.5.4)

За визначенням маємо

.

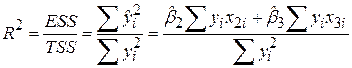(5.5.5)

Зазначимо, що можна отримати й інший вираз для R², якщо застосувати (5.5.3) і розділити обидві частини на 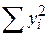. Одержимо

.

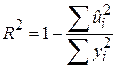R², як і R², лежить між 0 і 1. Якщо R²=1, то лінія регресії на 100% пояснює варіацію в Y. Якщо ж R²=0, модель нічого не пояснює у варіації Y. Проте R² зазвичай лежить між цими граничними величинами. Вважається, що підгонка моделі тим краща, чим більше R² наближається до 1.

Пригадаємо, що в моделі з двома змінними величина r позначала степінь лінійного зв’язку між двома змінними. У моделі з трьома й більше змінними аналогом r є коефіцієнт множинної кореляції, що позначається R. Він позначає степінь асоціативності між Y і всіма пояснювальними змінними одночасно. На відміну від r, який може бути і негативним, R набуває завжди позитивних значень. На практиці, проте, R відіграє незначну роль, більш важлива величина R².

Зазначимо зв’язок між R² і дисперсіями частинних коефіцієнтів регресії в моделі множинної регресії з k змінними (5.4.20):

,

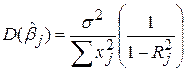(5.5.6)

де 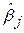– частинний коефіцієнт регресії при регресорі 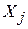, а 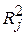– R² в регресії 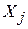по тих (k–2) змінних, що залишилися регресорами (у регресійній моделі з k змінними є (k–1) регресор). Ця рівність є узагальнення формул (5.4.12), (5.4.15) для моделі з трьома змінними (один регресант і два регресори).