Зауваження щодо стохастичної складової
Розглянемо модель регресії, у якій порівняно з (4.4.1) відсутня стохастична складова:
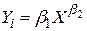 . .
| (4.7.1) |
З метою проведення регресійного аналізу цю модель можна подати в трьох різних видах:
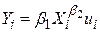 ; ;
| (4.7.2) |
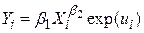 ; ;
| (4.7.3) |
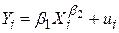 . .
| (4.7.4) |
Після логарифмування цих рівнянь одержуємо
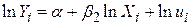 ; ;
| (4.7.5) |
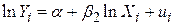 ; ;
| |
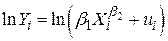 , ,
|
де 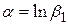 .
.
Модель типу (4.7.2) приводиться до лінійної (за параметрами) моделі регресії в тому розумінні, що шляхом відповідного перетворення (логарифмування) вона може бути приведена до лінійної щодо параметрів 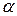 і
і 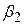 моделі. Зазначимо, що вона нелінійна щодо параметра
моделі. Зазначимо, що вона нелінійна щодо параметра 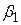 .
.
Хоча моделі (4.7.2) і (4.7.3) є лінійними моделями регресії і їх оцінка може проводитися за МНК, слід велику увагу приділити властивостям стохастичної складової, що входить у модель . Пригадаємо, що властивість якнайкращої лінійної незміщеної оцінки за МНК вимагає, щоб стохастична складова 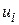 мала математичне сподівання, яке дорівнює нулю, постійну дисперсію та нульову автокореляцію. При перевірці гіпотез ми також припускаємо, що
мала математичне сподівання, яке дорівнює нулю, постійну дисперсію та нульову автокореляцію. При перевірці гіпотез ми також припускаємо, що 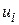 розподіляється за нормальним законом розподілу з математичним сподіванням і дисперсією, згаданими вище, тобто припускаємо, що
розподіляється за нормальним законом розподілу з математичним сподіванням і дисперсією, згаданими вище, тобто припускаємо, що 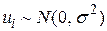 .
.
Звернемося до моделі (4.4.2). Логарифмічне перетворення приводить її до вигляду (4.4.5). Для використання класичної лінійної моделі регресії необхідно зробити припущення про те, що
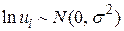 . .
| (4.7.6) |
Отже, коли ми проводимо регресію за моделлю (4.7.5), то 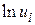 повинен бути розподілений за нормальним законом розподілу з нульовим математичним сподівання і постійною дисперсією. У такому разі
повинен бути розподілений за нормальним законом розподілу з нульовим математичним сподівання і постійною дисперсією. У такому разі 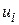 в (4.7.2) розподілений за логарифмічно-нормальним законом розподілу з математичним сподіванням
в (4.7.2) розподілений за логарифмічно-нормальним законом розподілу з математичним сподіванням 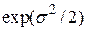 і дисперсією
і дисперсією 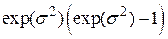 .
.
Дата добавления: 2016-07-27; просмотров: 1793;











