Алгоритми визначення максимального потоку

На підставі властивостей двоїстості задач лінійного програмування, як це показано в попередніх розділах, можливо визначити максимальний потік в мережі. Однак більш простішим є алгоритм Форда-Фалкерсона.

Розглянемо алгоритм отримання максимального потоку з любого початкового потоку. Ця процедура складається з двох операцій: операції А – процесу розташування поміток в вершинах мережі (графу) і операції В – зміни потоку. В наявності є кілька модифікацій методу поміток, в які закладена одна і та ж ідея: шляхом певної системи поміток визначаються ланцюги (шляхи), які не містять насичених дуг. Помітка починається з джерела (початку) х₀, яка помічається індексом 0, тобто 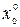. Нехай задана вже помічена вершина х_і (рис. 6). Якщо для деякої поміченої вершини х_і є суміжна вершина х_j, яка з’єднується з нею насиченою дугою, то остання вершина не помічається (рис. 6, а). Якщо слідуючи вершина з’єднана з поміченою х_і дугою зі значенням потоку 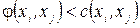, то вершина х_j помічається знаком +і, тобто 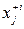(рис. 6, б).

Якщо вершина х_j пов’язана з х_і з позитивним нульовим потоком 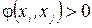, то вона позначається знаком -і, тобто 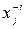(рис. 6, в). Таким чином, не помічаються такі вершини, які з’єднані з поміченою суміжною вершиною х_і виходячи з неї насиченою дугою, або дугою з нульовим потоком, що входить в неї (рис. 6, г).

Ясно, що потік в мережі можна збільшити за рахунок збільшення потоків в дугах, що закінчуються вершинами, поміченими знаком "+" і зменшення потоків дугах, що закінчуються в вершинах, помічених знаком "–". На рис. 7 наведено приклад поміченого шляху.

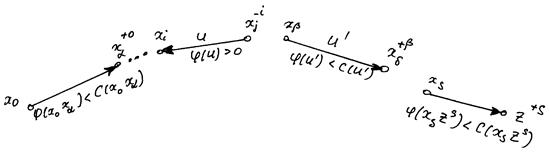
Рис. 7. Приклад поміченого шляху

Припустимо, що процедурі помічення вершин, вдалося знайти такий шлях (всі вершини його помічені), що в нього попала кінцева вершина. Тоді така ситуація називається прорив (по одному із шляхів прорвалися до кінця). В протилежному випадку кажуть про не прорив. Це означає, що між початком х₀ і кінцем х_z є шлях 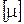, вершини якого помічені індексами попередніх вершин. Тоді можливо збільшити потік в мережі. Справді, так як знайдений шлях 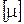не містить в собі жодної прямої насиченої дуги, то можна змінити значення потоків на всіх дугах цього шляху на величину

,

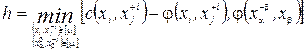причому потік на дузі збільшується на h, якщо орієнтація дуги співпадає з напрямком від х₀ до х_z і зменшується на 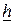в протилежному випадку. Після цього отримуємо новий потік, збільшений на величину h. Далі всі помітки на вершинах графу зтираються і процедура повторюється спочатку. Цей процес повторюють до тих пір, доки неможливо знайти жодного шляху 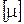, тобто до не прориву. На цьому останньому кроці ми отримуємо максимальний потік. Слід зауважити, що існують і інші форми запису алгоритму, наприклад [28]. Початкова вершина помічається 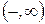. Суміжна наступна вершина х_j помічається 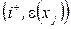, якщо

,

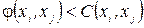де 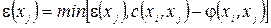. (2.1)

або ця вершина помічається 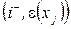, якщо 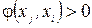, де

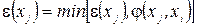. (2.2)

Процедуру отримання максимального потоку рекомендується починати з нульового значення потоку.

Приклад. Визначимо максимальний потік в мережі, яка наведена на рис... Біля кожної дуги проставлена її пропускна спроможність. Послідовний процес розв’язку наводиться в таблиці.

Таблиця

Дуги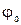

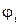
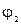
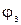
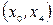
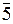
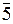
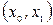
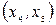
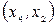
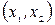
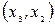
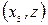
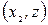
В цьому простому прикладі без особливої праці можна знайти шлях від х₀ до z, який не містить насичених дуг. Таким є шлях 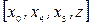. У відповідності з формулою (2.1) збільшуємо значення потоку на дугах цього шляху на 2 тоді дуга 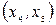стає насиченою (в табл. це відмічено рискою зверху). Відповідні значення потоку наведені в третьому стовпчику табл. На другій ітерації вибираємо другий шлях 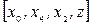, вільний від насичених дуг.

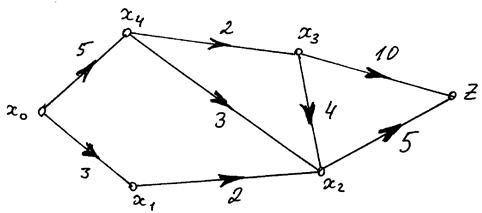
Рис. 8 Пояснення до прикладу

Змінюємо (збільшуємо) значення потоку на 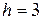. Сумарний потік наведений в четвертому стовпчику. На третій ітерації вибирається шлях 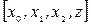, потік збільшується на 2. результати наведені в п’ятому стовпчику. Прорив з точки z більше ніяким чином здійснити неможливо. Отриманий потік є максимальним зі значенням Ф=7.

Приклад. Проілюструємо метод поміток вершин на прикладі мережі, що наведена на рис. 9, а. Джерелу х₀ надаємо мітку 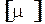. Далі, вершині х₂ надаємо мітку 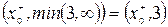. Це єдина вершина, яку можна помітити, починаючи з х₀, тому що дуга (х₀, х₁) є насиченою. Продовжуючи процес з х₂ можемо помітити вершину х₁ двома способами: 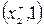або 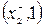. Настав прорив, рис. 9, б. Вздовж розглянутого шляху 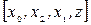значення 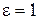. Змінюємо на це значення потоки на дугах. Отримуємо новий потік зі значенням сумарного потоку на кінцевих дугах 2 (замість початкового, який дорівнював 1), який представлений на рис. 9, в. Далі знов проходить прорив вздовж шляху 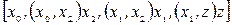. Після зміни потоків на 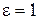маємо потік, який наведений на рис. 9, г, з максимальним значенням потоку на кінцевих дугах 3. мінімальний розріз складається з дуг .

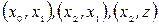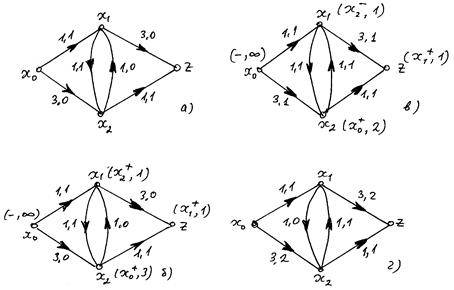
Рис. 9 Пояснення до прикладу.

Угорський алгоритм

а) задачі, які розв’язуються угорським алгоритмом.

Відома визначена кількість задач управління, які розв’язуються за допомогою спеціального алгоритму, який названий по роботам Куна, угорським [1, 3, 28].

Цей алгоритм базується на принципі двоїстості і теоремі про максимальний потік.

Для його застосування необхідно, щоб задача зводилась до певного математичного формулювання, і, загалом, щоб граф задачі, що наводиться на рис. 10, тобто структурне зображення задачі мало вигляд графа, що складається окрім початкової і кінцевої вершин з підмножин внутрішніх "парних" вершин, що з’єднуються між собою дугами.

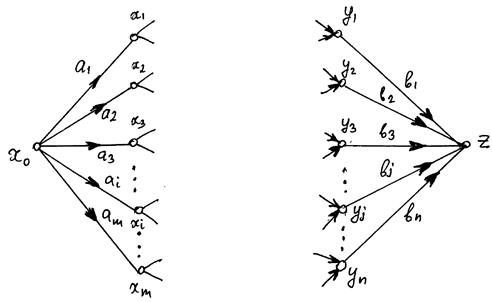
Рис. 10 Вид типового графа для задач,

що розв’язуються угорським алгоритмом

Розглянемо декілька задач, які мають такий граф, який називається інколи простим або дводольним.

Транспортна задача Хічкока. Задано m портів відправлення х₁ і n портів призначення y_j; кількість суден a_i, яке повинно бути відправлено в порту і; кількість суден b_j. Яке повинно прийти в порт j і транспортні витрати d_ij при перевезенні вантажу між портами х_і і у_j. Необхідно визначити кількість суден 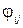, щоб сукупні витрати на перевезення були мінімальними:

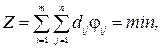(2.3)

при умовах

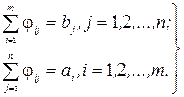(2.4)

є інше формулювання задачі Хічкока, де рівності (2.4) і рівняння балансу

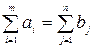
замінюються нерівностями

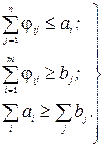(2.5)

Задачу в формі нерівностей, можливо звести до рівностей якщо до матриці 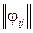добавити ще один 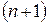-й стовпчик, із сумою елементів, що дорівнює різниці

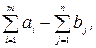
і вважати .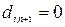

При цьому істотною є умова .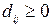

Транспортна задача Ордена. Є надлишок а_і товарів в m пунктах 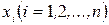і попит b_і в n пунктах .

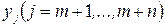Задані пропускні спроможності 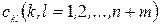між пунктами і транспортні витрати 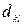по транспортуванню із одного пункту до іншого. Потрібно визначити оптимальні значення кількостей товару 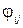, які потрібно перевозити, щоб сумарні транспортні витрати були мінімальними

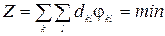, (2.6)

при умовах рівності сукупних надлишків товарів і загального попиту

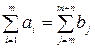, (2.7)

Задача розв’язується при таких обмеженнях:

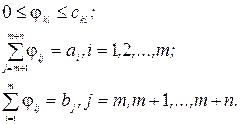(2.8)

Задача про оптимальне призначення. Потрібно призначити працівника х_і на деякий станок (операцію) y_i 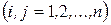. Задана продуктивність праці 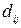працівника х_і на операцію y_i. Вважається, що 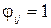, якщо працівник х_і призначається на операцію y_i і 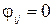в протилежному випадку. Потрібно максимізувати сукупну продуктивність праці

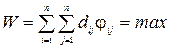, (2.9)

при обмеженнях

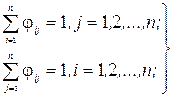(2.10)

Обмеження (2.10) означає, що забороняється праця декількох робітників на даній операції, і одного працівника на кількох операціях.

Зведемо три розглянуті задачі до єдиного математичного формулювання. Будемо вважати, що у всіх задачах потрібно максимізувати функцію

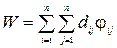(2.11)

при обмеженнях

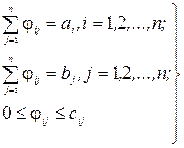(2.12)

Задачу мінімізації можна звести в загальному випадку до задачі максимізації одним з двох шляхів. По-перше можна замість змінних 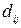ввести величини

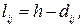(2.13)

де

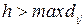. (2.14)

якщо розглянути тотожність

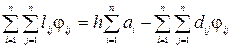, (2.15)

то мінімізація виразу, який має вигляд (2.13) аналогічно максимізації правої частини (2.15). Другий шлях полягає в заміні коефіцієнтів (2.11) на протилежні по знаку, тобто вводяться нові змінні .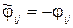

В ряді випадків (задача про мінімальний шлях) від’ємні значення потоку не є перепоною до розв’язку задачі.

Задача Хічкока зводиться до стандартної форми, якщо замість величини 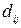ввести 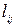у відповідності до (2.13) і вважати, що .

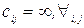Для задачі про оптимальні призначення необхідно в формулах (2.11) і (2.12) вважати

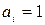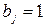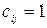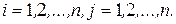, , ; (2.16)

Це означає, що 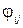може приймати тільки два значення 0 і 1 в силу умови цілочисельності потоку.

Стандартна задача зображається графом з рис.10.

Вершини х_і це пункти відправлення, або працівники, 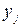– пункти призначення, або операції. В цей граф добавлені початкова і кінцева вершини, які поєднуються дугами з пропускними спроможностями 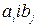, де

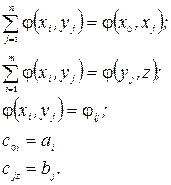(2.17)

Цей граф відображає топологічні властивості нашої логістичної або кібернетичної задачі.

Задача про найкоротший шлях (або про критичний шлях). Існує транспортна мережа. Кожній дузі (х, у) або (х_і, у_j) поставлена у відповідність деяка величина – довжина дуги 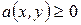. Потрібно знайти шлях із початкової х₀ в кінцеву вершину z, який має найкоротшу довжину. Вочевидь, ця задача зводиться до задачі про потік мінімальної вартості, якщо позначити:

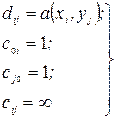(2.18)

причому

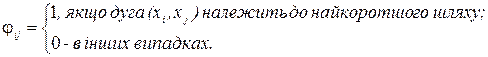
Під довжиною шляху можна розуміти довжину шляху (відстань); кількість палива, яке витрачається при русі по цій ділянці; вартість проїзду по даній ділянці і т.ін.

В задачах сіткового планування (мережевого планування) дуже часто зустрічається задача визначення критичного шляху. Люба складна, комплексна робота або розробка зображується у вигляді сіткового графіка, який являє собою транспортну мережу. Точка х₀ – початок роботи, вершина Z – її закінчення. Окремі види робіт (операції) зображуються дугами, вершина х_і – початок операції, x_j – момент її завершення. Кожній дузі ставиться у відповідність число 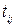– тривалість виконання роботи, кожній вершині х_і – час 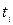початку даної роботи.

Потрібно знайти такий шлях з початкової вершини до кінцевої, вздовж якого сумарний час виконання робіт був би максимальним. Такий шлях називають критичним. Без його зменшення неможливо скоротити загальний час виконання робіт. Критичних шляхів може бути декілька. Тоді для скорочення загального часу всього комплексу робіт, потрібно скоротити тривалість робіт, що входять в критичний шлях.

Якщо взяти до розгляду ще й вартості виконання робіт, то в данному критичному шляху потрібно скорочувати ті роботи, які дають найменший приріст вартості при скороченні тривалості їх виконання робіт від часу через 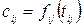, то скорочувати потрібно ті роботи критичного шляху, для яких похідна 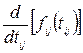максимальна. Після скорочення одного критичного шляху може з’явитися інший.

Дану задачу можна звести до пошуку потоку мінімальної вартості, якщо замість часу виконання робіт 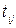ввести величини

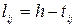(2.19)

де

,

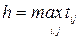або розглядати від’ємні величини

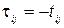. (2.20)

б) формальний виклад угорського алгоритму

Після того, як були розглянуті задачі, що зводяться до знаходження потоку мінімальної вартості в мережі, розглянемо сутність угорського алгоритму. Будемо вважати, що є транспортна мережа, яка складається з двох підмножин вершин: 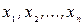і 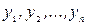, а також початкової х₀ і кінцевої z. Вважаються відомими пропускні спроможност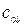і і 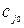дуг, які з’єднують х₀ з вершинами х_i і вершини у_j з кінцевою 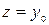. Для дуг 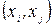, які з’єднують вершини х_i з у_j задані 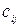. Необхідно знайти потік 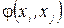, який насичує вихідні дуги, тобто такий потік, який задовольняє обмеженням

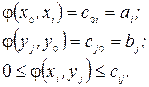
і надає максимуму лінійній формі

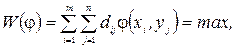(2.24)

де 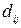– відомі константи

дану задачу можна представити у вигляді мережі, яка зображена на рис.... Аналогічно до задачі про потік максимальної вартості можна отримати, якщо врахувати співвідношення (2.17). Співвідношення (2.21) і (2.22) означає, що спочатку розглядається потік, що насичує крайні (вхідні і вихідні) дуги.

Вираз (2.24) називається роботою потоку. При цьому величини 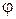ототожнюються з напругою деякого силового поля, а 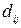– із зарядом джерела [3]. Таким чином, потрібно знайти потік, що насичує вихідні дуги і здійснює максимальну роботу.

Поруч із основною задачею, що задається формулами (2.21)–(2.24), розглядаємо двоїсту задачу. Для цього задамо на дугах мережі G функцію бюджет

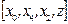(2.25)

таку, що

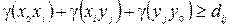(2.26)

В двоїстій задачі потрібно мінімізувати лінійну форму

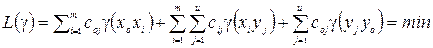(2.27)

Функція L ( 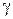) має назву спроможності бюджету 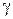. Співвідношення (2.26) можна пояснити наступним чином. Якщо трактувати 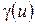як кількість коштів (грошей), яку потрібно сплатити за всі транспортні засоби перевезення по шліху, то співвідношення (2.26) означає, що ця величина не повинна бути менше найбільшої повної вартості роботи d_ij, яка здійснюється, коли транспорт курсує по шляху 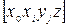. Введемо більш зручні позначення:

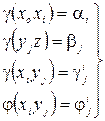(2.28)

З теореми двоїстості виходить, що W( 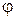) 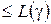. Це можна зразу встановити, якщо замітити що співвідношення (2.26) можна переписати у вигляді:

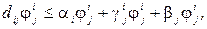
(2.29)

звідки, взявши подвійні суми від лівої і правої частин

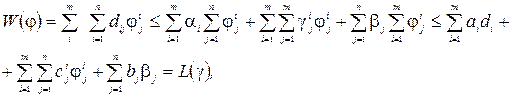(2.30)

тому, що у відповідності до закону збереження потоку

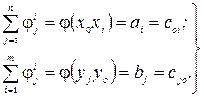
(2.31)

Звідси, так як і в теоремі про максимальний потік, якщо знайдеться такий потік j і бюджет g, що

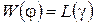, (2.32)

то j буде шуканим розв’язком, яке максимізує роботу.

Спочатку будемо вважати, що всі 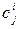нескінченні, тоді 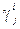повинні дорівнювати нулю.

Двоїста задача тепер полягає в тому, щоб знайти такі числа 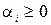і 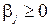, для яких

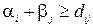
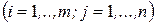(2.33)

Поруч з основною та двоїстою розглянемо допоміжну задачу, яка полягає в наступному. Кожному бюджету 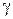співставимо допоміжну транспортну мережу 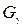, яка отримується з початкової мережі G видаленням тих дуг 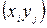, для яких

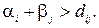(2.34)

Потрібно знайти максимальний потік по транспортній мережі

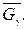
Наведемо дві теореми для мережі .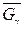

Теорема 2.1. Якщо при бюджеті 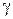мережа 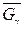пропускає потік 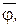що насичує вихідні дуги цієї мережі (або G), то 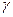- бюджет з найменшою спроможністю, а 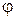- потік в мережі G, що здійснює найбільшу роботу.

Вочевидь, якщо 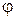є потоком в мережі G і насичує вихідні дуги цієї мережі G, то він є максимальним для мереж 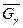і G. Зауважимо, що вихідні дуги мережі G всі включені в мережу 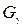, тому що включаються тільки внутрішні дуги 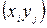для яких 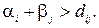Далі, на дугах, для яких 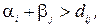значення потоку 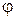береться нульовим, то на тих дугах, що залишилися 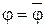, тобто

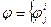при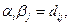

0 при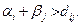

Робота цього потоку дорівнює

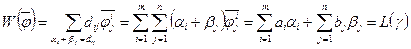(2.35)

В цьому співвідношенні додавання ведеться тільки по тим дугам, для яких

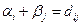
(2.36)

(тобто по таким дугам, які б увійшли в ).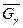

Теорема 2.2. Якщо при бюджеті 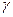мережа 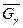не допускає потоку 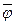, що насичує її вихідні дуги, то можна знайти новий бюджет 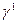із спроможністю L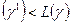

Нехай 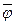- максимальний потік в мережі 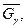який не насичує вихідні дуги в мережі. Згідно теореми про максимальний потік значення сумарного потоку на скінчених дугах цього потоку дорівнює пропускній спроможності того розрізу Г 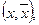якого він насичує. Нехай розріз Г 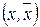визначається множиною вершин ( рис 11,а):

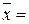
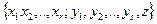
Так як Г 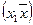– розріз з найменшою пропускною спроможністю, то він не містить дуг з нескінченною пропускною спроможністю і тому із співвідношення і > r і 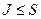виходить, що дуга 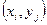не входить в мережу 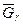, так як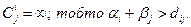

Очевидно, що дуги 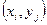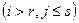належить розрізу Г 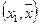, так як один кінець дуги 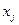; другий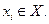

З формул (2.33) і (2.34) ясно, що всі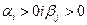

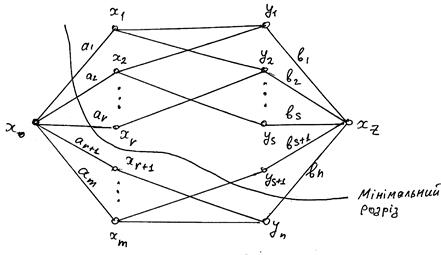
"так"

"ні"

Рис. 11 Пояснення до угорського алгоритму

а) мінімальний розріз б) блок-схема алгоритму

Тоді змінимо значення 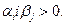у відповідності до формул

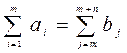(2.37)

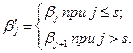(2.38)

Величини 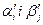створюють бюджет, тому що вони задовольняють обмеженням (2.33). Дійсно, якщо і 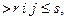то

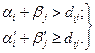
Спроможність нового бюджету дорівнює

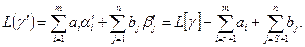
Звідси

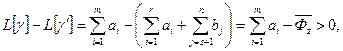(2.40)

де 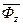– величина сумарного потоку на кінцевих дугах мережі 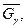яка дорівнює пропускній спроможності розрізу (рис. 11 а), тобто

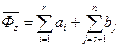
і цей потік не насичує вихідні дуги, тому в (2.40) стоїть знак >, що і потрібно було довести. Для пояснення формули (2.40) потрібно повернутися до рис 11 а. Розріз перетинає початкові дуги при 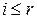і кінцеві при 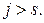Інші дуги можна не включати в розріз, тому, що розрізання кінцевих дуг все рівно перериває потік, а внутрішні дуги має нескінченно велику пропускну спроможність.

Для побудови алгоритму знаходження потоку (рис. 11 б),який проводить максимальну роботу, при умові 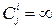будемо робити наступним чином. Виходимо з бюджету

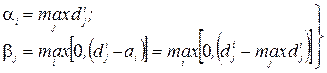(2.41)

Очевидно, що значення 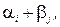які задовольняють співвідношенню (2.36) і ввійти в мережу 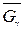. Далі шукають максимальний потік в цьому графі. Якщо він насичує вихідні дуги, то задача розв’язана. Якщо ні, то по формулам (2.37) і (2.38) визначаємо новий бюджет 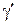і повторюємо всю процедуру. Аналогічна процедура проводиться для 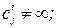і в цьому випадку тепер потрібно врахувати величину 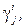які тепер тотожньо не дорівнюють нулю. Очевидно, що можна вважати

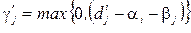(2.42)

Поруч з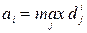

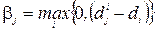(2.43)

При цьому всі величини 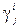невід’ємні.

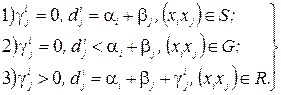(2.44)

Як видно з (2.44) всі ці три випадки відповідають умові (2.26)

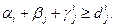
Введемо мережу 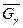, яка має ті ж дуги, що і мережа G, але пропускна спроможність визначається співвідношенням

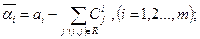(2.45)

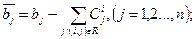(2.46)

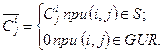(2.47)

Сума у співвідношенні (2.45) береться при фіксованому індексу і по всім j, таким, що дуга 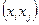належить множині R; в (2.46) – навпаки.

Тут так само як і в теоремі 2.2. можна вважати, що всі 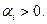Нехай

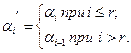(2.48)

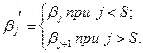(2.49)

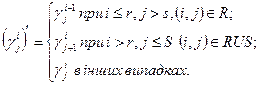(2.50)

Нові числа, які задаються формулами (2.48)-(2.50) визначають новий бюджет, тобто задовольняють обмеженню

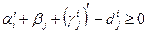(2.51)

Приклад 2. 3 Розглянемо мережу, яка зображена на рис. 12 а)

Задаємо коефіцієнти 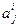у вигляді таблиці 2. 2.

і			І
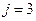
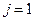
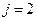
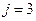
					< 0 < 0	< 0 < 0	< 0 < 0 < 0 < 0

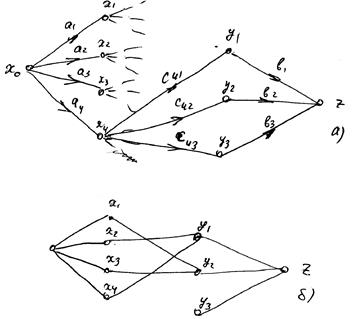
Рис. 12. Допоміжний граф мережі 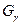в угорському алгоритмі.

Використовуючи співвідношення (2.42) і (2.43), отримуємо

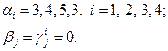
Далі за допомогою формули (44) визначаємо множини S, G, R – Для цього складемо таблицю значень різниць D =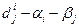

За допомогою цієї таблиці маємо, що

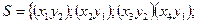
Q =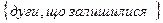

R =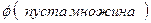

Тому у відповідності до формули (2.47) отримуємо пропускні спроможності дуг мережі :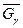

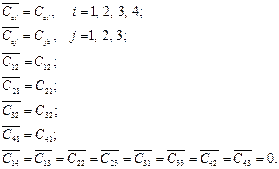
Мережа 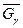що відповідає цим значенням, зображена на рисунку 12, б. В цій мережі за допомогою алгоритму Форда-Фалкерсона необхідно визначити максимальний потік.

Якщо цей потік насичує вихідні дуги, то задача розв’язана. Якщо насичення вихідних дуг не сталося, то по формулам (2.48)-(2.50) змінюють значення двоїстих змінних і повторюють процедуру знаходження максимального потоку і т. д.

Крім цього важливою задачею є задача визначення плану, що є оптимальним по вартостям. В даному посібнику ми на цій проблемі зупинятися не будемо, тому що ця задача є в більшому ступені відноситься до курсів “Дослідження операцій, “Математичне програмування” та “Операційний менеджмент”. Дана задача досить детально роз­гля­да­ється, наприклад в