Ілюстрований приклад. Крива Філіпса для Великобританії, 1950–1966 рр.
У табл. 4.5 наведені дані про щорічні темпи зростання заробітної плати Y і рівня безробіття Х у Великобританії в період 1950–1966 рр.
Таблиця 4.5
Темпи зростання зарплати й рівня
безробіття у Великобританії, 1950–1966 рр.
| Рік | Темп зростання зарплати, % | Рівень безробіття, % |
| 1,8 | 1,4 | |
| 8,5 | 1,1 | |
| 8,4 | 1,5 | |
| 4,5 | 1,5 | |
| 4,3 | 1,2 | |
| 6,4 | ||
| 1,1 | ||
| 1,3 | ||
| 3,6 | 1,8 | |
| 2,6 | 1,9 | |
| 2,6 | 1,5 | |
| 4,2 | 1,4 | |
| 3,6 | 1,8 | |
| 3,7 | 2,1 | |
| 4,8 | 1,5 | |
| 4,3 | 1,3 | |
| 4,6 | 1,4 |
Застосування моделі (4.6.1) дає такі результати:
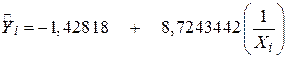 (2,067478) (2,8477792)
(2,067478) (2,8477792)  = 0,3849
t = (0,690782) (3,0635606) = 0,3849
t = (0,690782) (3,0635606)  = 9,3854
p = (0,500253) (0,0078824) p = (0,00788) = 9,3854
p = (0,500253) (0,0078824) p = (0,00788)
|
Згідно з цими результатами граничний рівень зниження зарплати за рік дорівнює –1,43%. Тобто, якщо Х необмежено зростає, зниження заробітної плати буде не більше ніж 1,43% на рік.
Як підсумок наведемо табл. 4.6, що містить основні результати розглянутих нами моделей.
Таблиця 4.6
Основні формули для нелінійних за змінними моделей
| Модель | Вигляд | Кутовий коефіцієнт 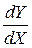
| Еластичність 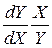
|
| Лінійна | 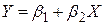
| 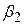
| 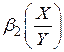
|
| Log-log | 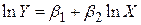
| 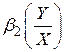
| 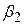
|
| Log-lin | 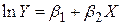
| 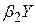
| 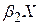
|
| Lin-log | 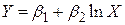
| 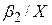
| 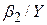
|
| Обернена | 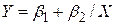
| 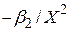
| 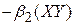
|
Якщо вираз для коефіцієнта еластичності залежить від змінних, то на практиці звичайно використовуються їх середні значення.
Дата добавления: 2016-07-27; просмотров: 1942;











