Дисперсія та стандартна похибка оцінювачів за МНК

Для отриманих значень частинних коефіцієнтів регресії можна вивести формули для дисперсії і стандартної похибки подібно до того, як це було зроблено для двовимірної моделі. Ці величини потрібні для двох основних завдань: встановлення довірчих інтервалів і перевірка статистичних гіпотез. Відповідні формули мають такий вигляд:

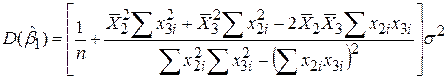;	(5.4.9)
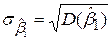;	(5.4.10)
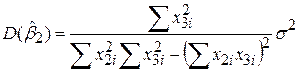,	(5.4.11)

або

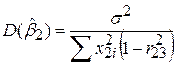,	(5.4.12)
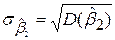;	(5.4.13)
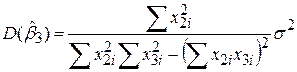,	(5.4.14)

або

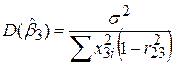;	(5.4.15)
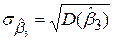;	(5.4.16)
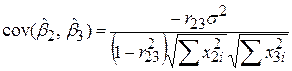,	(5.4.17)

де R²₃ – коефіцієнт кореляції між Х₂ і Х₃, що визначається за формулою

.

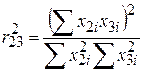У всіх цих формулах s² є гомоскедастична дисперсія збурень 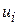. Можна показати, що незміщена оцінка для s² визначається за формулою

.

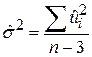(5.4.18)

Відзначимо аналогію між (5.4.18) і формулою для двовимірного випадку

.

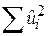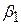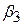Тепер кількість степенів вільності дорівнює (N–3), оскільки при оцінюванні ми повинні спочатку оцінити , і , які «поглинають» три степені вільності.

Для обчислення 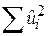з (5.4.18) можна застосувати більш просту для обчислень формулу

,

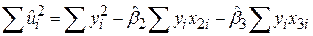(5.4.19)

що є тривимірним аналогом формули (2.3.6).

Дійсно, пригадаємо, що

,

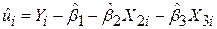або у формі відхилень від середніх величин

.

Тепер можемо виконати такі прості перетворення:

.

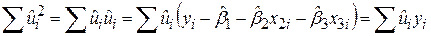При цьому нами застосована рівність

.

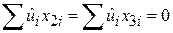Звідси маємо

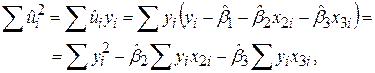
що доводить справедливість (5.4.19)