Припущення 2.2 - середні значення залишкових членів нульові

Кожна 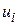- випадкова величина з .

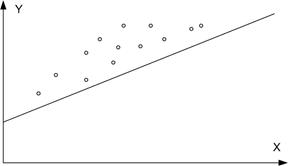
На рис. 2.3. бачимо, що деякі з точок спостереження лежать вище за лінію 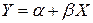, а деякі нижче. Це означає, що частина складових 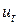позитивні, а інші негативні. Оскільки 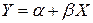- лінія середніх значень, доцільно припустити, що ці випадкові відхилення взаємно знищуються в середньому за всією популяцією. Отже, припущення про те, що 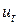- випадкові величини з нульовим математичним сподіванням, достатньо реалістичне.

Припущення 2.3 - не всі значення X однакові

Не всі 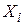мають однакові значення. Принаймні є два різних значення. Іншими словами, дисперсія вибірки 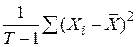відмінна від нуля.

Це припущення є дуже важливим, оскільки інакше модель не може бути оцінена. На інтуїтивному рівні, якщо 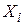не змінюється, то неможливо пояснити, чому змінюється 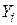. Як приклад, припустимо, що 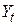- споживацькі витрати сім’ї в t–му місяці, а 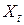- дохід сім’ї в тому ж місяці. Звичайно дохід сім’ї від місяця до місяця трохи змінюється, а споживацькі витрати можуть значно варіювати в різні місяці. Якщо дохід не змінюється, то не можна пояснити, чому змінюються витрати на споживання. Це, однак, не означає, що дохід сім’ї не впливає на її споживацькі витрати. Якщо наступного року зарплата підвищиться, то підвищаться й середні витрати. Рис. 2.4 графічно ілюструє припущення 2.3.

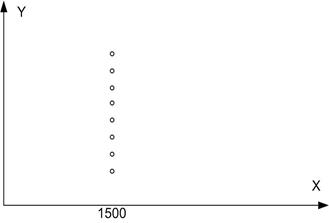
Рис. 2.4. Приклад, у якому величини X не змінюються

У разі застосування моделі, що описує вартість будинку залежно від його площі, припустимо, що була зібрана інформація про вартість будинків площею тільки 1500 кв. футів. Діаграма розкиду даних вибірки зображена на рис.2.4. Зрозуміло, що за цією діаграмою неможливо провести адекватну оцінку лінії регресії популяції.

Припущення 2.4 - значення X задані й невипадкові

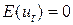, оскільки 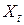задані і, отже, невипадкові, то з цього випливає .

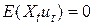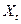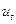З випливає, що коваріація популяції між і дорівнює нулю. Отже, X і u не корельовані. Як ми побачимо пізніше, це припущення є основоположним для того, щоб метод оцінювання 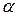і 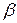мав деякі бажані властивості. На інтуїтивному рівні, якщо X і u корельовані, то зі зміною X повинна також змінюватися u. У цьому випадку очікуване значення Y не буде дорівнювати .

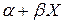Припущення 2.5 - гомоскедастичність

Усі випадкові величини 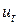мають однаковий розподіл дисперсій 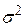, так що 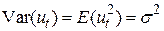. Ця властивість називається гомоскедастичністю (рівнорозкиданістю).

Припущення 2.6 - серійна незалежність

Усі 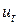розподілені незалежно, так що 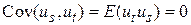для всіх 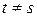. Ця властивість має назву серійної незалежності.

Виконання цих двох гіпотез приводить до того, що залишкові члени незалежно й однаково розподілені. Згідно з рис.1.2. для даного X є розкид значень Y, який задає умовний розподіл. Залишок 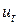- відхилення від умовного середнього значення 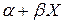. Припущення 2.5 має на увазі, що розподіл випадкової величини 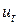має ту ж дисперсію ( 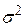), що й у для різних X спостережень S. Рис. 2.3 - приклад гетероскедастичності (нерівних розкидів), у якому дисперсія непостійна за спостереженнями. Припущення 2.6 говорить про те, що 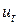і незалежні і, отже, не корельовані. Зокрема, послідовні складові не корельовані. Рис.2.5 - приклад серійної кореляції, коли це припущення порушується.

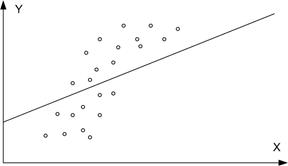
а б

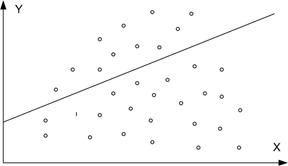
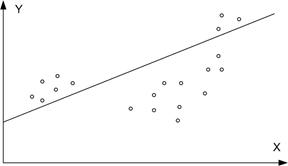
в г

Рис. 2.5. Приклади порушення припущень: а - порушення 2.2;

б- порушення 2.1; в - порушення 2.5; г- порушення 2.6

Припущення 2.7 - нормальність відхилень

Кожне 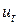розподілено нормально згідно із законом 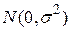, з чого виходить, що умовна густина розподілу Y для заданого значення X задається законом .

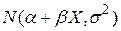Таким чином, залишкові складові 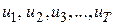вважаються розподіленими незалежно і за нормальним законом з нульовим середнім значенням і загальною дисперсією 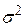. Це припущення дуже важливе при висуванні та перевірці гіпотез.

Класична лінійна регресійна модель: