Припущення 2 - величини X фіксовані в повторних вибірках
Значення, що набуваються регресором X, вважаються фіксованими в повторних вибірках. Безумовно, вважатимемо, що X не стохастична.
Це припущення неявно було присутнє в обговоренні PRF раніше. Дуже важливо розуміти значення «фіксованість» у повторних вибірках. Його можна пояснити на прикладі табл. 2.1. Розглянемо змінну Y, відповідну рівням доходу. Зберігаючи величину доходу фіксованою, наприклад на рівні 80 дол., ми випадково вибрали сім’ю з тижневими витратами, скажімо, у 60 дол. Зберігаючи X=80, ми випадково вибрали іншу сім’ю з Y=75. У кожному з цих випадків (повторні вибірки) значення X були фіксовані. Ми можемо повторити цей процес для всіх X з таблиці. Це означає, що регресійний аналіз є умовним регресійним аналізом, тобто з умовою заданості величин регресора X.
Припущення 3 - рівність нулю середньої величини збурення 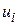
Для даного значення величини X середня величина або математичне сподівання випадкової збурюючої складової 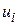 дорівнює нулю:
дорівнює нулю:
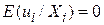
Це припущення стверджує, що середня величина 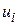 , відповідна даному
, відповідна даному 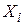 , є нуль.
, є нуль.
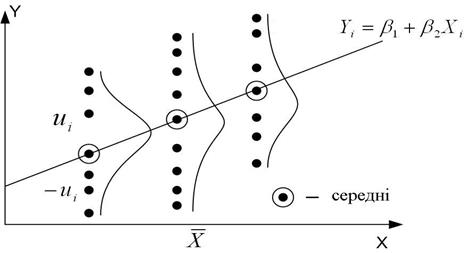
Рис. 2.6 Геометрична інтерпретація припущення 3
Геометричне значення цього припущення показане на рис. 2.6. Як бачимо, при фіксованому значенні Х відповідні значення Y розташовані довкола середніх значень, коли одні зі значень Y лежать вище середніх, а інші – нижче середніх. Відстані, вище і нижче за середні, є не що інше як 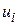 . За формулою (2.2.1), середня величина цих відхилень для фіксованого X повинна дорівнювати нулю.
. За формулою (2.2.1), середня величина цих відхилень для фіксованого X повинна дорівнювати нулю.
Припущення 4 - гомоскедастичність або рівність дисперсій 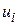
Для даного X дисперсії 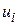 однакові для всіх спостережень:
однакові для всіх спостережень:
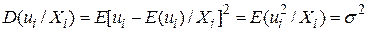 . .
| (2.2.4) |
Рівність (2.2.4) стверджує, що дисперсія 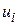 для кожного
для кожного 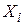 є деяка позитивна величина, що дорівнює
є деяка позитивна величина, що дорівнює 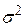 . Іншими словами, (2.2.4) означає, що величини Y,відповідні різним значенням Х,мають однакову дисперсію.
. Іншими словами, (2.2.4) означає, що величини Y,відповідні різним значенням Х,мають однакову дисперсію.
На рис. 2.7 показана ситуація, коли ця властивість не виконується, тобто коли має місце рівність
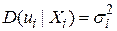 .
.
. 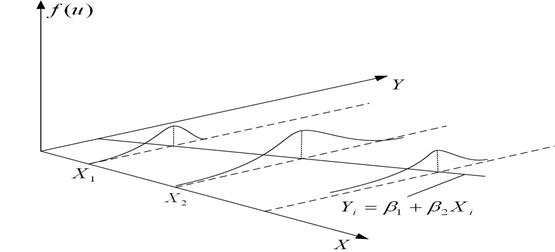
Рис. 2.7. Гомоскедастичність
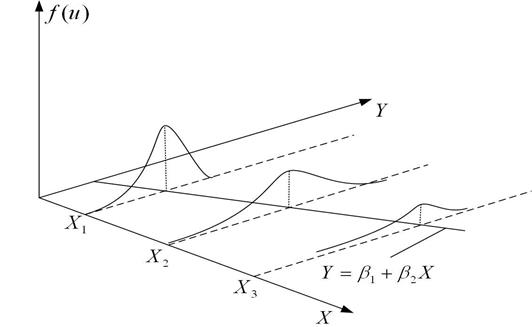
Рис. 2.8. Гетероскедастичність
Щоб краще зрозуміти різницю між двома цими ситуаціями, повернемося до нашого прикладу. Графіки 2.7 і 2.8 показують, що зі зростанням доходу зростають і середні витрати на споживання. Але на рис. 2.7 дисперсія (розкид) витрат однакова для всіх рівнів доходів, а на рис. 2.8 дисперсія витрат збільшується зі зростанням Х, тобто багаті сім'ї в середньому купують більше, ніж бідні, але в них і більший розкид у витратах, ніж у бідних.
На рис. 2.8 показано, що
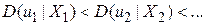
Дата добавления: 2016-07-27; просмотров: 1613;











