Властивості оцінок за МНК
1. Оцінки за МНК виражаються тільки через величини спостережуваних змінних X і Y. Унаслідок цього вони можуть бути легко обчислені за формулами (2.1.15) (2.1.16).
2. Ці оцінки є точковими, тобто для даної вибірки кожен оцінювач матиме єдину величину, визначувану спостережуваними значеннями. Надалі ми розглянемо так звані інтервальні оцінки, які дають інтервал можливих значень невідомих параметрів.
Відзначимо деякі властивості лінії SRF.
1. Лінія SRF проходить через середні значення вибірки X і Y, тобто через точку 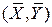 . Цей факт безпосередньо випливає з формули (2.1.16), якщо її перетворити до вигляду
. Цей факт безпосередньо випливає з формули (2.1.16), якщо її перетворити до вигляду
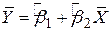 .
.
На рис. 2.2 показано, що лінія SRF проходить через точку 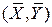 .
.
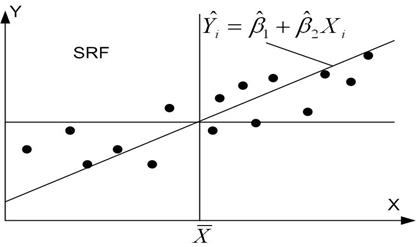
Рис. 2.2. Лінія SRF
2. Середня величина Y за наслідками вибірки дорівнює середній величині, отриманій із рівняння регресії 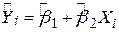 , тобто
, тобто
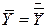 . .
| (2.2.1) |
Щоб довести це, виконаємо такі перетворення:
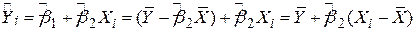 .
.
Ми підставили замість 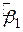 його вираз із (2.1.16). Підсумуємо обидві частини отриманої рівності за всім обсягом вибірки
його вираз із (2.1.16). Підсумуємо обидві частини отриманої рівності за всім обсягом вибірки
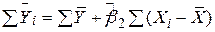 ,
,
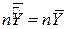 ,
, 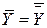 .
.
При цьому ми використовували властивість (2.1.12).
3. Середня величина залишків 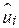 є нуль, тобто
є нуль, тобто 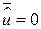 . Ця властивість виходить безпосередньо з (2.1.5) і (2.1.7). Використовуючи цю властивість, можна перетворити рівняння SRF
. Ця властивість виходить безпосередньо з (2.1.5) і (2.1.7). Використовуючи цю властивість, можна перетворити рівняння SRF
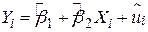
| (2.2.2) |
до іншого вигляду, в який будуть входити лише змінні у відхиленнях. Для цього підсумуємо останню рівність за всією вибіркою
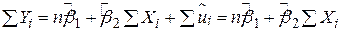 .
.
Поділивши останню рівність на N, одержуємо
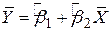 . .
|
Віднімемо цю рівність від (2.2.2):
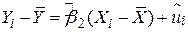
|
або
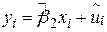 . .
| (2.2.3) |
Рівняння (2.2.3) називається рівнянням у відхиленнях. Зауважимо, що 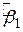 в це рівняння не входить. Рівняння SRF у відхиленнях можна подати у вигляді
в це рівняння не входить. Рівняння SRF у відхиленнях можна подати у вигляді
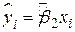 . .
| (2.2.3) |
4. Залишки 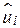 не корелюються з
не корелюються з 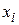 , тобто
, тобто 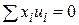 . Це твердження виходить безпосередньо з (2.1.6) і (2.1.7).
. Це твердження виходить безпосередньо з (2.1.6) і (2.1.7).
5. Залишки 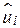 не корелюються з
не корелюються з 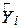 , тобто
, тобто 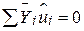 . Дійсно
. Дійсно
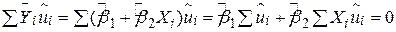 . .
|
6. Залишки 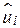 не корелюються з
не корелюються з 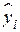 , тобто
, тобто 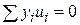 . Підставляючи замість
. Підставляючи замість 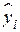 його значення з (2.2.3), одержуємо
його значення з (2.2.3), одержуємо
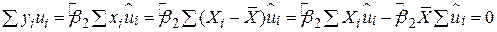 . .
|
Дата добавления: 2016-07-27; просмотров: 1712;











