Експериментальне визначення SRF

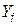
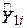
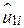
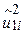
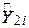
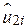
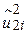
1	2	3	4	5	6	7	8
		2.929	1.071	1.147
		7.000	–2.000	4.000		–2
		8.357	–1.357	1.841		–1
		9.714	2.286	5.226
Сума: 28			0.000	12.214

Зауваження: 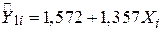(тобто , ),

, , .

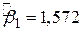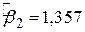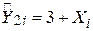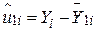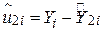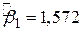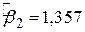Проведемо два експерименти. В експерименті 1 покладемо і (зараз ми не говоримо про те, як ми отримали ці значення, припустимо ми просто вгадали). Застосовуючи ці значення та величини X, подані в колонці 2, ми легко можемо визначити оцінку 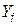, наведену в колонці 3 як 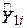(індекс 1 позначає перший експеримент). Проведемо другий експеримент, поклавши цього разу 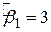і 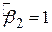(оцінки величини 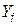при цьому наведені в колонці 6). Оскільки 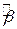- величини у двох експериментах різні, ми маємо два різні значення для суми квадратів залишків (як відомо з таблиці); 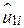– залишки за першим експериментом, а 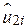– за другим (квадрати цих залишків наведені в колонках 5 і 8). З наведених у таблиці даних бачимо, що, як і очікувалося з (2.1.3), суми квадратів залишків у двох експериментах різні, оскільки вони базуються на різних 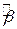- величинах.

Тепер виникає питання, які 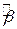-величини нам слід вибрати? Оскільки 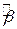-величини в першому експерименті дають меншу величину 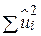(=12.214), ніж у другому (=14), ми можемо сказати, що 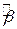– величини в першому експерименті «кращі», ніж у другому. Але чи «кращі» вони за всіма можливими значеннями? Якби ми мали необмежений час, то могли б багато разів проводити подібні експерименти, вибираючи різні 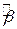-величини кожного разу й порівнюючи результуючу величину 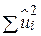. При цьому, зрозуміло, нам потрібно було б перебрати всі можливі значення 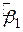і 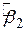. Але оскільки час обмежений, то потрібен більш поширений метод, ніж процедура спроб і помилок. На щастя, МНК дозволяє скористатися добре відомою процедурою знаходження мінімуму функції з двома змінними.

Для цього отримаємо вираз для функції 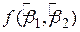з (2.1.3):

.

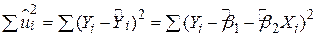(2.1.4)

З курсу вищої математики відомо, що функція (2.1.4) набуватиме якнайменшого значення при тих числових значеннях 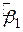і 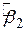, при яких перетворюються в нуль частинні похідн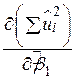і і 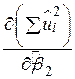. Обчислимо їх, пам’ятаючи, що і 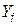не залежать від 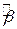-величин:

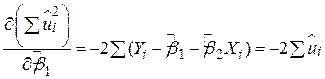
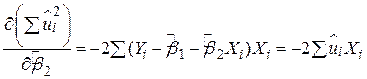
(2.1.5)     (2.1.6)

Зрівнюючи до нуля ці вирази, одержуємо таку систему двох лінійних алгебраїчних рівнянь щодо коефіцієнтів регресі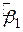ї і :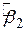

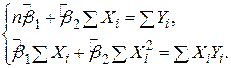
(2.1.7)

Отримаємо розв’язок цієї системи, застосовуючи, наприклад, формули Крамера:

;

;

;

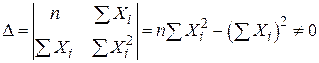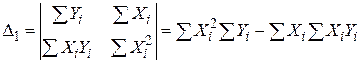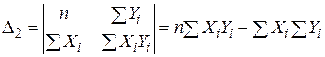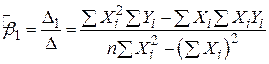;	(2.1.8)
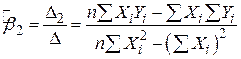.	(2.1.9)

Дведемо, що можна отримати більш прості вирази для коефіцієнтів регресії. Для цього введемо нові величини – відхилення від середніх за вибіркою значень

, ,

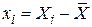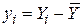(2.1.10)

де 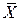і 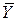позначають середні за вибіркою значення

, .

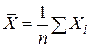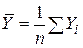З цих формул відразу випливають прості співвідношення

, .

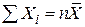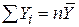(2.1.11)

Покажемо, що

, .

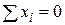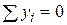(2.1.12)

Дійсно

.

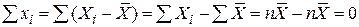Аналогічно доводиться і друга рівність. Окрім цього справедлива формула

.

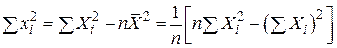(2.1.13)

Шляхом елементарних перетворень одержуємо

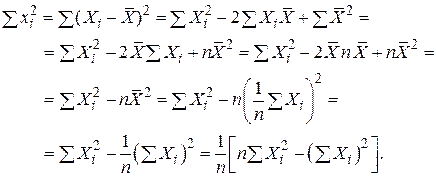
Порівнюючи вирази для 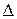і (2.1.13), можна помітити, що визначник 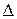відрізняється від нуля у випадку, якщо не всі мають однакові значення.

Наведемо ще одне співвідношення

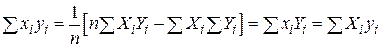
(2.1.14)

Доведення:

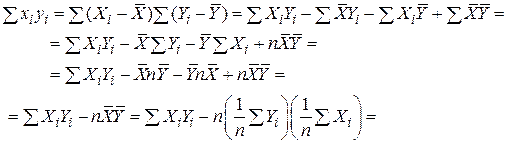
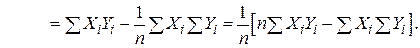
Водночас

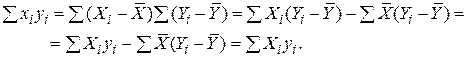
Звернемося тепер до виразу для 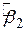(2.1.9). Застосовуючи (2.1.13) і (2.1.14), одержуємо

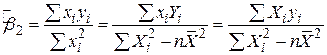
(2.1.15)

Спростимо тепер вираз (2.1.8) для 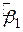. З першого рівняння системи (2.1.7) одержуємо

.

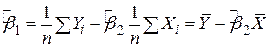(2.1.16)

У наступному пірозділі ми зупинимося на деяких властивостях оцінок, отриманих за методом найменших квадратів.