Дійсна й оцінена ціна будинку і його житлова площа у кв. футах
| t | SQFT | Дійсна ціна PRICE | Оцінена середня ціна |
| 1999,9 | 200,386 | ||
| 226,657 | |||
| 233,051 | |||
| 271,554 | |||
| 274,751 | |||
| 295,601 | |||
| 302,551 | |||
| 312,281 | |||
| 321,316 | |||
| 323,123 | |||
| 265,657 | |||
| 413,751 | |||
| 441,551 | |||
| 469,351 |
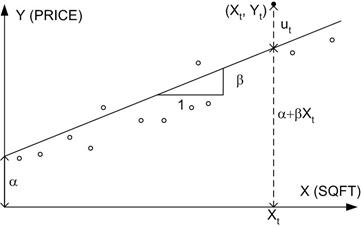
Рис. 2.3. Діаграма вибірки розкиду ціни будинку залежно від його площі
Фундаментальне припущення, на якому основана найпростіша регресійна модель, полягає в тому, що середні значення 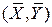 лежать на прямій лінії (позначеній
лежать на прямій лінії (позначеній 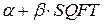 ), яка зображає функцію регресії популяції і є умовним середнім значенням (або сподіванням) ціни (PRICE) для заданої площі SQFT. Нижче наводиться загальне визначення найпростішої лінійної регресійної моделі.
), яка зображає функцію регресії популяції і є умовним середнім значенням (або сподіванням) ціни (PRICE) для заданої площі SQFT. Нижче наводиться загальне визначення найпростішої лінійної регресійної моделі.
Припущення 2.1 - лінійність моделі:
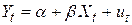 , ,
|
де 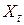 і
і 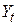 є t-тіспостереження (t змінюється від 1 до T) незалежної і залежної змінних відповідно;
є t-тіспостереження (t змінюється від 1 до T) незалежної і залежної змінних відповідно; 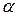 і
і 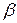 - невідомі параметри, які необхідно визначити;
- невідомі параметри, які необхідно визначити; 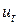 - невідома складова, яка передбачається випадковою величиною з певними властивостями.
- невідома складова, яка передбачається випадковою величиною з певними властивостями. 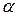 і
і 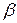 мають назву коефіцієнтів регресії. Індекс t можна визначити як тимчасовий чинник у спостереженнях або типове спостереження з таблиці.
мають назву коефіцієнтів регресії. Індекс t можна визначити як тимчасовий чинник у спостереженнях або типове спостереження з таблиці.
Припустимо, що нам відомі величини 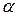 і
і 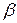 . Побудуємо пряму
. Побудуємо пряму 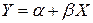 на цій діаграмі. Вона зображає функцію регресії популяції. Відхилення за вертикаллю дійсного значення ціни (
на цій діаграмі. Вона зображає функцію регресії популяції. Відхилення за вертикаллю дійсного значення ціни ( 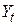 ) від лінії регресії (
) від лінії регресії ( 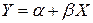 ) є випадкова похибка
) є випадкова похибка 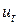 . Кутовий коефіцієнт прямої (
. Кутовий коефіцієнт прямої ( 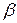 ) є також
) є також 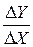 . Він позначає зростання Y при одиничному зростанні X.
. Він позначає зростання Y при одиничному зростанні X.
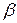 може бути інтерпретований як граничний ефект X на Y. Так, якщо
може бути інтерпретований як граничний ефект X на Y. Так, якщо 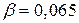 , то кожне збільшення житлової площі на 1 кв. фут призведе до зростання ціни будинку в середньому на 0,065 тис. дол. (зверніть увагу на важливість вибору одиниць вимірювання) або 65 дол. Більш імовірно, що зростання житлової площі на 100 кв. футів призведе до зростання очікуваної середньої ціни на 6 500 дол. Хоча
, то кожне збільшення житлової площі на 1 кв. фут призведе до зростання ціни будинку в середньому на 0,065 тис. дол. (зверніть увагу на важливість вибору одиниць вимірювання) або 65 дол. Більш імовірно, що зростання житлової площі на 100 кв. футів призведе до зростання очікуваної середньої ціни на 6 500 дол. Хоча 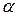 відповідає середньому значенню Y при X=0, його не можна інтерпретувати як вартість ділянки, на якій стоїть будинок. Пояснення цьому твердженню полягає в тому, що
відповідає середньому значенню Y при X=0, його не можна інтерпретувати як вартість ділянки, на якій стоїть будинок. Пояснення цьому твердженню полягає в тому, що 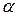 містить вплив невключених у модель змінних, які, проте, впливають на залежну змінну.
містить вплив невключених у модель змінних, які, проте, впливають на залежну змінну.
При формулюванні найпростішого лінійного співвідношення між PRICE і SQFT ми ігноруємо той факт, що ціна будинку залежить також від інших характеристик, таких як, наприклад, величина ділянки землі й кількість ванних. Таким чином, ми припускаємо, що ефекти від них абсорбуються залишковим членом 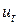 . Залишковий член
. Залишковий член 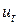 , є, по суті, комбінацією чотирьох різних ефектів:
, є, по суті, комбінацією чотирьох різних ефектів:
1. Відповідає за ефект дії змінних, не включених у модель.
2. Поглинає ефекти нелінійності співвідношення між Y і X. Так, якби істинною була модель 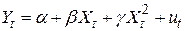 , а ми б застосовували модель 2.1, то ефект від
, а ми б застосовували модель 2.1, то ефект від 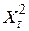 був би включений в
був би включений в 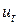 .
.
3. Містить похибку у вимірюванні X і Y.
4. Включає властиві непередбачувані випадкові ефекти.
Хоча досліджувана нами модель дуже проста і, звичайно, не реалістична, з її допомогою можна легко зрозуміти різні концепції в економетриці. Далі ми розширимо модель на випадок, коли в неї входять більше ніж одна пояснювальна змінна.
Наступною нашою задачею після формулювання моделі є отримання “найкращих” оцінок для 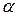 і
і 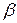 . Після того як це буде зроблено, ми перевіримо властивості цих оцінок, а також припущення 2.1. Потім перевіримо гіпотези, що належать до них, і застосуємо оцінену пряму для проведення умовного прогнозу ціни будинку для даного значення X. Але перш ніж ми все це виконаємо, нам необхідно зробити відносно
. Після того як це буде зроблено, ми перевіримо властивості цих оцінок, а також припущення 2.1. Потім перевіримо гіпотези, що належать до них, і застосуємо оцінену пряму для проведення умовного прогнозу ціни будинку для даного значення X. Але перш ніж ми все це виконаємо, нам необхідно зробити відносно 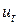 і
і 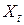 додаткові припущення. Нижче наведено повний список припущень.
додаткові припущення. Нижче наведено повний список припущень.
Припущення найпростішої лінійної регресійної моделі
1. Регресійна модель лінійна по відношенню до невідомих коефіцієнтів 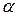 і
і 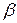 , тобто
, тобто 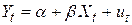 для t=1, 2, ..., T.
для t=1, 2, ..., T.
2. Залишкова складова 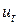 - випадкова величина, що має нульове середнє значення, тобто
- випадкова величина, що має нульове середнє значення, тобто 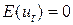 .
.
3. Не всі із спостережуваних значень X мають однакову величину, принаймні одне з них відрізняється від інших.
4. 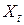 задані й невипадкові, тобто вони не корелюються з
задані й невипадкові, тобто вони не корелюються з 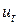 , отже,
, отже, 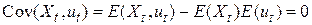 .
.
5. 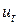 має сталу дисперсію для всіх t, тобто
має сталу дисперсію для всіх t, тобто 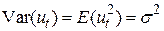 .
.
6. 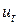 і
і  розподілені незалежно для
розподілені незалежно для 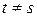 , звідси
, звідси 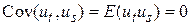 .
.
7. 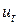 розподілена нормально, тобто
розподілена нормально, тобто 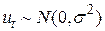 . Це означає, що для даного
. Це означає, що для даного 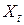
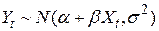 .
.
Розглянемо ці припущення більш детально.
Дата добавления: 2016-07-27; просмотров: 1601;











